Difference between revisions of "Manuals/calci/EXPONDIST"
Jump to navigation
Jump to search
| Line 4: | Line 4: | ||
*<math>cu</math> is the logical value like TRUE or FALSE | *<math>cu</math> is the logical value like TRUE or FALSE | ||
| − | == | + | ==Description== |
| + | *This function gives the exponential distribution. This distribution used to model the time until something happens in the process. *This describes the time between events in a Poisson process i.e., a process in which events occur continuously and independently at a constant average rate. | ||
| + | *For e.g Time between successive vehicles arrivals at a workshop. | ||
| + | *In EXPONDIST(x, lambda,cu), xis the value of the function, lambda is called rate parameter and cu(cumulative) is the TRUE or FALSE. *This function will give the cumulative distribution function , when cu is TRUE,otherwise it will give the probability density function , when cu is FALSE. | ||
| + | *Suppose we are not giving the cu value, by default it will consider the cu value is FALSE. | ||
| + | *This function will give the error result when | ||
| + | 1. x or λ is non-numeric. | ||
| + | 2. x<0 or λ<=0 | ||
| + | The probability density function of an exponential distribution is: f(x;λ)={λe^-λx , x>=0 | ||
| + | 0 , x<0 | ||
| + | or f(x;λ)= λ e^-λ x .H(x) | ||
| + | |||
| + | *where λ is the rate parameter and H(x) is the Heaviside step function | ||
| + | *This function is valid only on the interval [0,infinity). | ||
| + | The cumulative distribution function is :F(x,λ)={1-e^-λ x, x>=0 | ||
| + | 0 , x<0 | ||
| + | or :F(x,λ)=1-e^-λ x.H(x). | ||
| + | |||
| + | *The mean or expected value of the exponential distribution is: E[x]=1/ λ. | ||
| + | *The variance of the exponential distribution is:Var[x]=1/ λ^2. | ||
| + | |||
| + | == | ||
EXPONDIST is to model the time between events. | EXPONDIST is to model the time between events. | ||
Revision as of 23:12, 28 November 2013
EXPONDIST(x,Lambda,cum)
- is the value of the function
- is the value of the rate parameter
- is the logical value like TRUE or FALSE
Description
- This function gives the exponential distribution. This distribution used to model the time until something happens in the process. *This describes the time between events in a Poisson process i.e., a process in which events occur continuously and independently at a constant average rate.
- For e.g Time between successive vehicles arrivals at a workshop.
- In EXPONDIST(x, lambda,cu), xis the value of the function, lambda is called rate parameter and cu(cumulative) is the TRUE or FALSE. *This function will give the cumulative distribution function , when cu is TRUE,otherwise it will give the probability density function , when cu is FALSE.
- Suppose we are not giving the cu value, by default it will consider the cu value is FALSE.
- This function will give the error result when
1. x or λ is non-numeric.
2. x<0 or λ<=0
The probability density function of an exponential distribution is: f(x;λ)={λe^-λx , x>=0
0 , x<0
or f(x;λ)= λ e^-λ x .H(x)
- where λ is the rate parameter and H(x) is the Heaviside step function
- This function is valid only on the interval [0,infinity).
The cumulative distribution function is :F(x,λ)={1-e^-λ x, x>=0
0 , x<0 or :F(x,λ)=1-e^-λ x.H(x).
- The mean or expected value of the exponential distribution is: E[x]=1/ λ.
- The variance of the exponential distribution is:Var[x]=1/ λ^2.
== EXPONDIST is to model the time between events.
X or Lambda must be a numeric value in this function. Otherwise it shows error.
If x is less than 0, or Lambda less than or equal to zero, EXPONDIST shows error value.
AVEDEV (N1, N2...)
Where N1, N 2 ... are positive integers.
Let’s see an example
EXPONDIST(x, Lambda, cum)
B
0.5
15
=EXPONDIST (B2, B3, TRUE) is 0.9994
=EXPONDIST (0.5, 15, FALSE) is 0.0083
 is the value of the function
is the value of the function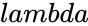 is the value of the rate parameter
is the value of the rate parameter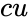 is the logical value like TRUE or FALSE
is the logical value like TRUE or FALSE