Difference between revisions of "Manuals/calci/BETADIST"
Jump to navigation
Jump to search
| Line 5: | Line 5: | ||
==Description== | ==Description== | ||
| − | *This function gives the | + | *This function gives the Cumulative Beta Probability Density function. |
| − | *The beta distribution is a family of | + | *The beta distribution is a family of Continuous Probability Distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by <math>\alpha</math> and <math>\beta</math>. |
| − | *The Beta | + | *The Beta Distribution is also known as the Beta Distribution of the first kind. |
| − | *In BETADIST(x,alpha, | + | *In BETADIST(x,<math>\alpha</math>,<math>\betab</math>,a,b) <math>x</math> is the value between <math>a</math> and <math>b</math>. |
| − | *Normally x | + | *alpha is the value of the shape parameter. |
| − | *The | + | *beta is the value of the shape parameter |
| − | *The formula for the | + | *<math>a</math> and <math>b</math>(optional) are the Lower and Upper limit to the interval of <math>x</math>. |
| − | F(x)=Ix( | + | *Normally <math>x</math> lies between the limit <math>a</math> and <math>b</math>, suppose when we are omitting <math>a</math> and <math>b</math> value, by default <math>x</math> value with in 0 and 1. |
| + | *The Probability Density Function of the beta distribution is: | ||
| + | <math>f(x)=\frac{x^{\alpha-1}(1-x)^{ \beta-1}}{B(\alpha,\beta)},</math> where <math>0 /le x /le 1</math>; <math>/alpha,/beta >0 </math> and <math>B(\alpha,\beta)</math> is the Beta function. | ||
| + | *The formula for the Cumulative Beta Distribution is called the Incomplete Beta function ratio and it is denoted by <math>Ix</math> and is defined as : | ||
| + | <math>F(x)=Ix(\alpha,\beta)=\int_{0}^{x}{t^{α−1}(1−t)^{\beta−1}dt} {B(p,q)}, where <math>0 \le x \le 1</math>0 ; <math>\alpha,\beta>0</math>0 and <math>B(\alpha,\beta)</math> is the Beta function. | ||
*This function will give the result as error when | *This function will give the result as error when | ||
| − | 1. Any one of the arguments are non-numeric | + | 1.Any one of the arguments are non-numeric |
| − | 2.alpha or beta< | + | 2.<math>\alpha \le 0</math> or <math>\beta \le 0</math> |
| − | 3.x<a ,x>b, or a=b | + | 3.<math>x<a</math> ,<math>x>b</math>, or <math>a=b</math> |
| − | 4. we are not mentioning the limit values a and b, by default it will consider the standard cumulative beta distribution, a= 0 and b= 1. | + | 4.we are not mentioning the limit values <math>a</math> and <math>b</math>, by default it will consider the standard cumulative beta distribution, <math>a = 0</math> and <math>b = 1</math>. |
==Examples== | ==Examples== | ||
Revision as of 04:06, 3 December 2013
BETADIST(x,alpha,beta,a,b)
- x is the value between a and b,
- alpha and beta are the value of the shape parameter
- a & b the lower and upper limit to the interval of x.
Description
- This function gives the Cumulative Beta Probability Density function.
- The beta distribution is a family of Continuous Probability Distributions defined on the interval [0, 1] parameterized by two positive shape parameters, denoted by and .
- The Beta Distribution is also known as the Beta Distribution of the first kind.
- In BETADIST(x,,Failed to parse (unknown function "\betab"): {\displaystyle \betab} ,a,b) is the value between and .
- alpha is the value of the shape parameter.
- beta is the value of the shape parameter
- and (optional) are the Lower and Upper limit to the interval of .
- Normally lies between the limit and , suppose when we are omitting and value, by default value with in 0 and 1.
- The Probability Density Function of the beta distribution is:
where ; and is the Beta function.
- The formula for the Cumulative Beta Distribution is called the Incomplete Beta function ratio and it is denoted by and is defined as :
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x)=Ix(\alpha,\beta)=\int_{0}^{x}{t^{α−1}(1−t)^{\beta−1}dt} {B(p,q)}, where <math>0 \le x \le 1} 0 ; 0 and is the Beta function.
- This function will give the result as error when
1.Any one of the arguments are non-numeric 2. or 3. ,, or 4.we are not mentioning the limit values and , by default it will consider the standard cumulative beta distribution, and .
Examples
- BETADIST(0.4,8,10) = 0.359492343
- BETADIST(3,5,9,2,6) = 0.20603810250
- BETADIST(9,4,2,8,11) = 0.04526748971
- BETADIST(5,-1,-2,4,7) = NAN
See Also
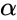 and
and 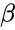 .
. is the value between
is the value between  and
and 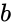 .
.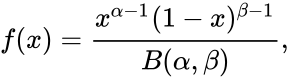 where
where 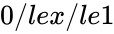 ;
; 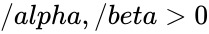 and
and 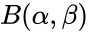 is the Beta function.
is the Beta function.
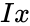 and is defined as :
and is defined as :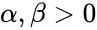 0 and
0 and 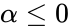 or
or 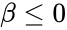 3.
3.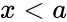 ,
,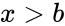 , or
, or 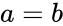 4.we are not mentioning the limit values
4.we are not mentioning the limit values 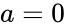 and
and 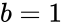 .
.