Difference between revisions of "Manuals/calci/CHIINV"
Jump to navigation
Jump to search
| Line 10: | Line 10: | ||
*The <math>\chi^2</math> static used to compare the observed value in each table to the value which would be the expected under the assumption. | *The <math>\chi^2</math> static used to compare the observed value in each table to the value which would be the expected under the assumption. | ||
*If X has the chi-squared distribution with \nu degrees of freedom, then according to the first definition, 1/X has the Inverse-chi-squared distribution with \nu degrees of freedom; | *If X has the chi-squared distribution with \nu degrees of freedom, then according to the first definition, 1/X has the Inverse-chi-squared distribution with \nu degrees of freedom; | ||
| − | *If CHIDIST(x,df)=prob, then CHIINV(prob,df)= x. | + | *If <math>CHIDIST(x,df)=prob</math>, then <math>CHIINV(prob,df)= x</math>. |
| − | *CHIINV use the iterating method to find the value of x.suppose the iteration has not converged after 100 searches, then the function gives the error result. | + | *CHIINV use the iterating method to find the value of <math>x</math>.suppose the iteration has not converged after 100 searches, then the function gives the error result. |
*This function will give the error result when | *This function will give the error result when | ||
| − | Any one of the arguments are non-numeric | + | 1.Any one of the arguments are non-numeric |
| − | df value is not an integer | + | 2.<math> df</math> value is not an integer |
| − | + | 3.<math> df < 1 </math>or <math>df>10^10</math> | |
| − | Also prob<0 or prob>1. | + | Also <math> prob < 0 </math> or <math>prob>1</math>. |
==Examples== | ==Examples== | ||
Revision as of 05:48, 3 December 2013
CHIINV(prob,df)
- Where is the probability value associated with the Chi-squared Distribution
- is the number of Degrees of Freedom
Description
- This function gives the inverse value of One_tailed probability of the Chi-squared Distribution.
- It is called Inverted-Chi-square Distribution and it is a Continuous Probability Distribution of a positive-valued random variable.
- Degrees of freedom =.
- The static used to compare the observed value in each table to the value which would be the expected under the assumption.
- If X has the chi-squared distribution with \nu degrees of freedom, then according to the first definition, 1/X has the Inverse-chi-squared distribution with \nu degrees of freedom;
- If , then .
- CHIINV use the iterating method to find the value of .suppose the iteration has not converged after 100 searches, then the function gives the error result.
- This function will give the error result when
1.Any one of the arguments are non-numeric 2. value is not an integer 3.or Also or .
Examples
- CHIINV(0.0001234098,2)=18
- CHIINV(0.2547876,5)=6.56699
- CHIINV(0.157299207050,1)=2
- CHIINV(0.6785412,-1)=NAN
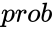 is the probability value associated with the Chi-squared Distribution
is the probability value associated with the Chi-squared Distribution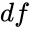 is the number of Degrees of Freedom
is the number of Degrees of Freedom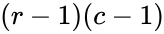 .
.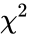 static used to compare the observed value in each table to the value which would be the expected under the assumption.
static used to compare the observed value in each table to the value which would be the expected under the assumption.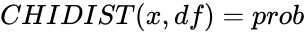 , then
, then 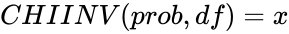 .
. .suppose the iteration has not converged after 100 searches, then the function gives the error result.
.suppose the iteration has not converged after 100 searches, then the function gives the error result.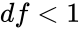 or
or 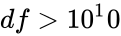 Also
Also 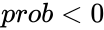 or
or 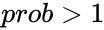 .
.