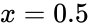Difference between revisions of "Manuals/calci/EXPONDIST"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''EXPONDIST(x,lambda, | + | <div style="font-size:30px">'''EXPONDIST(x,lambda,cu)'''</div><br/> |
*<math>x</math> is the value of the function | *<math>x</math> is the value of the function | ||
*<math>lambda(\lambda)</math> is the value of the rate parameter | *<math>lambda(\lambda)</math> is the value of the rate parameter | ||
Revision as of 03:19, 4 December 2013
EXPONDIST(x,lambda,cu)
- is the value of the function
- is the value of the rate parameter
- is the logical value like TRUE or FALSE
Description
- This function gives the Exponential Distribution. This distribution used to model the time until something happens in the process.
- This describes the time between events in a Poisson process i.e, a process in which events occur continuously and independently at a constant average rate.
- For e.g Time between successive vehicles arrivals at a workshop.
- In EXPONDIST(x, lambda,cu), xis the value of the function, lambda is called rate parameter and cu(cumulative) is the TRUE or FALSE. *This function will give the cumulative distribution function , when cu is TRUE,otherwise it will give the probability density function , when cu is FALSE.
- Suppose we are not giving the cu value, by default it will consider the cu value is FALSE.
- This function will give the error result when
1. or is non-numeric. 2. or
The Probability Density Function of an Exponential Distribution is
or
- Failed to parse (syntax error): {\displaystyle f(x;\lambda)= λe^{-\lambda x} .H(x)}
- where is the rate parameter and H(x) is the Heaviside step function
- This function is valid only on the interval [0,infinity].
The Cumulative Distribution Function is :
or
- The mean or expected value of the Exponential Distribution is: Failed to parse (syntax error): {\displaystyle E[x]=\frac{1}{ λ}}
- The variance of the Exponential Distribution is: .
Examples
Question : If jobs arrive at an average of 15 seconds, per minute, what is the probability of waiting 30 seconds, i.e 0.5 min? Here and
- =EXPONDIST(0.5,5,TRUE) = 0.917915001
- =EXPONDIST(5,3,TRUE) = 0.999999694
- =EXPONDIST(0.4,2,FALSE) = 0.898657928"
 is the value of the function
is the value of the function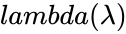 is the value of the rate parameter
is the value of the rate parameter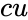 is the logical value like TRUE or FALSE
is the logical value like TRUE or FALSE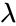 is non-numeric.
2.
is non-numeric.
2. 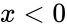 or
or 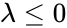
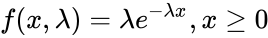
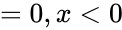
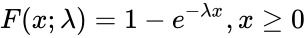
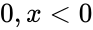
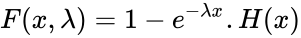
![{\displaystyle Var[x]={\frac {1}{\lambda ^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/da4e14dd45f1b281b9ec9a6a39cf48a24fc0776b) .
.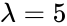 per minute, what is the probability of waiting 30 seconds, i.e 0.5 min?
Here
per minute, what is the probability of waiting 30 seconds, i.e 0.5 min?
Here