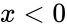Difference between revisions of "Manuals/calci/GAMMALN"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''GAMMALN(x)'''</div><br/> | <div style="font-size:30px">'''GAMMALN(x)'''</div><br/> | ||
| − | * | + | *<math>x</math> is the number |
==Description== | ==Description== | ||
| − | *This function gives | + | *This function gives the natural logarithm of the absolute value of the Gamma Function. |
| − | *The functions | + | *The functions Digamma and Trigamma are the first and second derivatives of the logarithm of the Gamma Function. |
| − | *This is often called the | + | *This is often called the ‘Polygamma’ function. |
| − | *Normally the number e to the power GAMMALN(x), where x is an integer, is same as (x-1)!. *GAMMALN=LN(GAMMA(x)) | + | *Gamma, Lgamma, Digamma and Trigamma functions are internal generic primitive functions. |
| − | *This function will give the result as error when x is | + | *Normally the number <math>e</math> to the power <math>GAMMALN(x)</math>, where <math>x</math> is an integer, is same as <math>(x-1)!</math>. |
| + | *<math>GAMMALN=LN(GAMMA(x))</math>, where: | ||
| + | <math>GAMMA(x) = \int\limits_{0}^{\infty} t^{x-1} e^{-t} dt</math> | ||
| + | and it is for all complex numbers except the negative integers and zero. | ||
| + | *This function will give the result as error when | ||
| + | <math>x</math> is non-numeric and <math>x \le 0</math>. | ||
==Examples== | ==Examples== | ||
| − | #GAMMALN(6)=4.787491744416229 | + | #GAMMALN(6) = 4.787491744416229 |
| − | #GAMMALN(42)=114.03421178146174 | + | #GAMMALN(42) = 114.03421178146174 |
| − | #GAMMALN(1)=0.00018319639111644828(calci) | + | #GAMMALN(1) = 0.00018319639111644828(calci) |
| − | #GAMMALN(-10)=NAN,because x<0 | + | #GAMMALN(-10) = NAN, because <math> x<0 </math> |
==See Also== | ==See Also== | ||
*[[Manuals/calci/GAMMADIST | GAMMADIST ]] | *[[Manuals/calci/GAMMADIST | GAMMADIST ]] | ||
Revision as of 04:40, 4 December 2013
GAMMALN(x)
- is the number
Description
- This function gives the natural logarithm of the absolute value of the Gamma Function.
- The functions Digamma and Trigamma are the first and second derivatives of the logarithm of the Gamma Function.
- This is often called the ‘Polygamma’ function.
- Gamma, Lgamma, Digamma and Trigamma functions are internal generic primitive functions.
- Normally the number to the power , where is an integer, is same as .
- , where:
and it is for all complex numbers except the negative integers and zero.
- This function will give the result as error when
is non-numeric and .
Examples
- GAMMALN(6) = 4.787491744416229
- GAMMALN(42) = 114.03421178146174
- GAMMALN(1) = 0.00018319639111644828(calci)
- GAMMALN(-10) = NAN, because
 is the number
is the number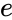 to the power
to the power 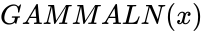 , where
, where 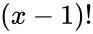 .
. , where:
, where:
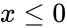 .
.