Difference between revisions of "Manuals/calci/CORREL"
Jump to navigation
Jump to search
| Line 19: | Line 19: | ||
==Examples== | ==Examples== | ||
| − | #1. Find the correlation coefficients for X and Y values are given below : | + | #1. Find the correlation coefficients for X and Y values are given below :X={1,2,3,4,5}; Y={11,22,34,43,56} |
| − | X={1,2,3,4,5}; Y={11,22,34,43,56} | ||
CORREL(A4:A8,B4:B8)=0.99890610723867 | CORREL(A4:A8,B4:B8)=0.99890610723867 | ||
| − | #The following table gives the math scores and times taken to run 100 m for 10 friends: | + | #The following table gives the math scores and times taken to run 100 m for 10 friends:SCORE(X)={52,25,35,90,76,40}; TIME TAKEN(Y)={11.3,12.9,11.9,10.2,11.1,12.5}CORREL(A5:A10,B5:B10)= -0.93626409417769 |
| − | SCORE(X)={52,25,35,90,76,40}; TIME TAKEN(Y)={11.3,12.9,11.9,10.2,11.1,12.5} | + | #Find the correlation coefficients for X and Y values are given below :X={-4,11,34,87};Y={9,2,59,24} CORREL(A1:A4,B1:B4)=0.353184665607273 |
| − | CORREL(A5:A10,B5:B10)= -0.93626409417769 | ||
| − | #Find the correlation coefficients for X and Y values are given below : | ||
| − | |||
| − | CORREL(A1:A4,B1:B4)=0.353184665607273 | ||
==See Also== | ==See Also== | ||
Revision as of 07:15, 9 December 2013
CORREL(ar1,ar2)
- are the set of values.
Description
- This function gives the correlation coefficient of the 1st set(ar1) of values and 2nd set(ar2) of values.
- Correlation is a statistical technique which shows the relation of strongly paired variables.
- For example ,test average and study time are related;those who spending time more to study they will get high marks and spending less time for studies their Average will goes down.
- There are different correlation techniques measuring the degree of correlation.
- The most common of these is the Pearson correlation coefficient denoted by r xy.
- The main result of a correlation is called the correlation coefficient (or "r")which ranges from -1 to +1.
- The r value is positive i.e.+1 when the two set values increase together then it is the perfect positive correlation.
- The r value is negative i.e. (-1) when one value decreases as the other increases then it is called negative correlation.
- Suppose the r value is 0 then there is no correlation (the values don't seem linked at all).
- If we have a series of n measurements of X and Y written as xi and yi where i = 1, 2, ..., n, then the sample *correlation coefficient is: CORREL(X,Y)= r xy=[ summation(i=1 to n)(xi-x(bar))(yi-y(bar))]/ SQRT{ summation(i=1 to n)(xi-x(bar))^2 summation(i=1 to n)(yi-y(bar))^2], where x(bar) and y(bar) are the sample means of X and Y. *This function will give the result as error when
- ar1 and ar2 are nonnumeric or different number of data points.
- ar1 or ar2 is empty
- The denominator value is zero.
- Suppose ar1 and ar2 contains any text, logical values, or empty cells, like that values are ignored.
Examples
- 1. Find the correlation coefficients for X and Y values are given below :X={1,2,3,4,5}; Y={11,22,34,43,56}
CORREL(A4:A8,B4:B8)=0.99890610723867
- The following table gives the math scores and times taken to run 100 m for 10 friends:SCORE(X)={52,25,35,90,76,40}; TIME TAKEN(Y)={11.3,12.9,11.9,10.2,11.1,12.5}CORREL(A5:A10,B5:B10)= -0.93626409417769
- Find the correlation coefficients for X and Y values are given below :X={-4,11,34,87};Y={9,2,59,24} CORREL(A1:A4,B1:B4)=0.353184665607273
See Also
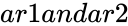 are the set of values.
are the set of values.