Difference between revisions of "Manuals/calci/FISHERINV"
Jump to navigation
Jump to search
| Line 4: | Line 4: | ||
*This function gives the inverse of the Fisher transformation. | *This function gives the inverse of the Fisher transformation. | ||
*We can use when the testing of correlations between set of data. | *We can use when the testing of correlations between set of data. | ||
| − | *The Inverse of the Fisher transformation is: <math>x= (e^2y-1)/(e^2y+1) i.e.,y=FISHER(x</math>), then | + | *The Inverse of the Fisher transformation is: <math>x= (e^2y-1)/(e^2y+1) i.e.,y=FISHER(x</math>), then FISHERINV(y)=x. |
*It can be used to construct a confidence interval. | *It can be used to construct a confidence interval. | ||
A confidence interval (CI) is a type of interval estimate of a population parameter and is used to indicate the reliability of an estimate. | A confidence interval (CI) is a type of interval estimate of a population parameter and is used to indicate the reliability of an estimate. | ||
Revision as of 07:28, 9 December 2013
FISHERINV(y)
- is the number.
Description
- This function gives the inverse of the Fisher transformation.
- We can use when the testing of correlations between set of data.
- The Inverse of the Fisher transformation is: ), then FISHERINV(y)=x.
- It can be used to construct a confidence interval.
A confidence interval (CI) is a type of interval estimate of a population parameter and is used to indicate the reliability of an estimate.
- This function will give the result as error when the y value is nonnumric.
Examples
- FISHERINV(0.6389731838)=0.56419999998
- FISHERINV(0)=0
- FISHERINV(0.1234)=0.1227774315035342
- FISHERINV(1)=0.761594155955765
- FISHERINV(-0.4296)=-0.4049869686465480
See Also
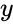 is the number.
is the number.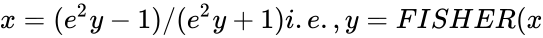 ), then FISHERINV(y)=x.
), then FISHERINV(y)=x.