Difference between revisions of "Manuals/calci/FISHER"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
*It is mainly associated with the Pearson Product-Moment Correlation coefficient for bi-variate normal observations. | *It is mainly associated with the Pearson Product-Moment Correlation coefficient for bi-variate normal observations. | ||
*In <math>FISHER(X)</math>, <math>x</math> is the number which ranges between -1 to +1. | *In <math>FISHER(X)</math>, <math>x</math> is the number which ranges between -1 to +1. | ||
| − | *The transformation is defined by : <math>z=\frac{1}{2} ln(1+\frac{x}{1-x})= arctanh(x)</math> | + | *The transformation is defined by : <math>z=\frac{1}{2} ln(1+\frac{x}{1-x})= arctanh(x)</math> |
| + | where <math>ln</math> is the natural logarithm function and <math>arctanh</math> is the Inverse Hyperbolic function. | ||
*This function will give the result as error when: | *This function will give the result as error when: | ||
1.<math>x</math> is non-numeric | 1.<math>x</math> is non-numeric | ||
Revision as of 00:12, 10 December 2013
FISHER(x)
- is the number.
Description
- This function gives the value of Fisher Transformation at .
- Fisher Transformation is used to test the hypothesis of two correlations.
- It is mainly associated with the Pearson Product-Moment Correlation coefficient for bi-variate normal observations.
- In , is the number which ranges between -1 to +1.
- The transformation is defined by :
where is the natural logarithm function and is the Inverse Hyperbolic function.
- This function will give the result as error when:
1. is non-numeric 2. or .
Examples
- FISHER(0.5642) = 0.6389731838284958
- FISHER(0)= 0
- FISHER(-0.3278) = -0.3403614004970268
- FISHER(1) = Infinity
- FISHER(-1) = Infinity
 is the number.
is the number.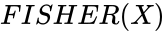 ,
, 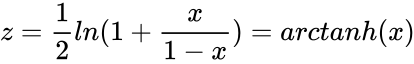
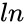 is the natural logarithm function and
is the natural logarithm function and 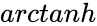 is the Inverse Hyperbolic function.
is the Inverse Hyperbolic function.
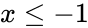 or
or 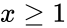 .
.