Difference between revisions of "Manuals/calci/HARMEAN"
Jump to navigation
Jump to search
| Line 15: | Line 15: | ||
==Examples== | ==Examples== | ||
| − | HARMEAN(1,2,3,4,5)=2.18978102189781 | + | #HARMEAN(1,2,3,4,5)=2.18978102189781 |
| − | HARMEAN(20,25,32,41)=27.4649361523969 | + | #HARMEAN(20,25,32,41)=27.4649361523969 |
| − | HARMEAN(0.25,5.4,3.7,10.1,15.2)=1.0821913906985883 | + | #HARMEAN(0.25,5.4,3.7,10.1,15.2)=1.0821913906985883 |
| − | HARMEAN(3,5,0,2)=NAN | + | #HARMEAN(3,5,0,2)=NAN |
| − | HARMEAN(1,-2,4)=NAN | + | #HARMEAN(1,-2,4)=NAN |
==See Also== | ==See Also== | ||
Revision as of 01:11, 10 December 2013
HARMEAN(n1,n2)
- and are the positive real numbers.
Description
- This function gives the harmonic mean of a given set of numbers.
- Harmonic mean is used to calculate the average of a set of numbers.
- The Harmonic mean is always the lowest mean.
- Normally Harmonic mean<geometric mean<Arithmetic mean.
- Harmonic mean is dfined by the reciprocal of the arithmetic mean of the reciprocals of a specified set of numbers.
- The harmonic mean of a positive real numbers x1,x2,x3....xn>0 is defined by H=n/(1/x1+1/x2+...+1/xn)=n/summation (i=1 to n)(1/xi).
- In HARMEAN(n1,n2,...) n1,n2.. are the positive real numbers, and here n1 is required.n2,n3..., are optional.
- Also arguments can be numbers,names, arrays or references that contain numbers.
- We can give logical values and text representations of numbers directly. Suppose the arguments contains any text, logical values or empty cells like that values are ignored.
- This will give the result as error when 1.the arguments with the error values or the referred text couldn't translated in to numbers.
2.Also any data point<=0.
Examples
- HARMEAN(1,2,3,4,5)=2.18978102189781
- HARMEAN(20,25,32,41)=27.4649361523969
- HARMEAN(0.25,5.4,3.7,10.1,15.2)=1.0821913906985883
- HARMEAN(3,5,0,2)=NAN
- HARMEAN(1,-2,4)=NAN
See Also
 and
and 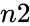 are the positive real numbers.
are the positive real numbers.