Difference between revisions of "Manuals/calci/IMPRODUCT"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''IMPRODUCT(z1,z2,z3)'''</div><br/> | <div style="font-size:30px">'''IMPRODUCT(z1,z2,z3)'''</div><br/> | ||
*<math>z1,z2,z3</math> are the complex numbers of the form <math>a+ib</math> | *<math>z1,z2,z3</math> are the complex numbers of the form <math>a+ib</math> | ||
| − | + | ||
==Description== | ==Description== | ||
| − | *This function gives the | + | *This function gives the product of the complex numbers. |
| − | * | + | *In IMPRODUCT(z1,z2,z3,…),Where z1,z2,z3,... are the complex numbers is in the form of "a+ib".i.e. |
| − | *i' | + | *a&b are the real numbers.'i' imaginary unit .<math>i=sqrt(-1)</math>. |
| − | *Then the | + | *The multiplication of two complex numbers is a complex number. |
| − | * | + | *Let z1=a+ib and z2=c+id. |
| − | *We can use COMPLEX function to convert real and imaginary number in to a complex number | + | *Then the product of two complex number is <math>z1.z2=(a+ib)(c+id)=(ac-bd)+(ad+bc)i</math> . |
| − | + | *In this function z1 is required.z2,z3,..., are optional. | |
| − | + | *We can use COMPLEX function to convert real and imaginary number in to a complex number. | |
==Examples== | ==Examples== | ||
| − | + | IMPRODUCT("1+3i","5+2i")=-1+17i | |
| − | + | IMPRODUCT("i","3-i")=1+3i | |
| − | + | IMPRODUCT("5","-2+4i")=-10+20i | |
| − | + | IMPRODUCT("2+3i","4+6i","3+5i")=-150+22i(EXCEL)=-10+24i(CALCI) | |
| + | IMPRODUCT("-6-2i","-1-i")=4+8i | ||
| − | * | + | *CALCI is not taking the third value for multiplication. |
| + | *It only applied for two numbers | ||
==See Also== | ==See Also== | ||
Revision as of 05:11, 17 December 2013
IMPRODUCT(z1,z2,z3)
- are the complex numbers of the form
Description
- This function gives the product of the complex numbers.
- In IMPRODUCT(z1,z2,z3,…),Where z1,z2,z3,... are the complex numbers is in the form of "a+ib".i.e.
- a&b are the real numbers.'i' imaginary unit ..
- The multiplication of two complex numbers is a complex number.
- Let z1=a+ib and z2=c+id.
- Then the product of two complex number is .
- In this function z1 is required.z2,z3,..., are optional.
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
Examples
IMPRODUCT("1+3i","5+2i")=-1+17i IMPRODUCT("i","3-i")=1+3i IMPRODUCT("5","-2+4i")=-10+20i IMPRODUCT("2+3i","4+6i","3+5i")=-150+22i(EXCEL)=-10+24i(CALCI) IMPRODUCT("-6-2i","-1-i")=4+8i
- CALCI is not taking the third value for multiplication.
- It only applied for two numbers
See Also
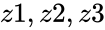 are the complex numbers of the form
are the complex numbers of the form 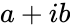
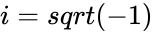 .
.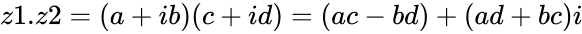 .
.