Difference between revisions of "Manuals/calci/IMARGUMENT"
Jump to navigation
Jump to search
| Line 9: | Line 9: | ||
*<math>I</math> imaginary unit .<math>i=\sqrt{-1}</math>. | *<math>I</math> imaginary unit .<math>i=\sqrt{-1}</math>. | ||
*An argument of the complex number <math>z = x + iy</math> is any real quantity <math>\psi</math> such that <math>z = x + i y</math> = <math>r cos(\psi) + i r sin(\psi)</math> for some positive real number <math>r</math>. | *An argument of the complex number <math>z = x + iy</math> is any real quantity <math>\psi</math> such that <math>z = x + i y</math> = <math>r cos(\psi) + i r sin(\psi)</math> for some positive real number <math>r</math>. | ||
| − | *Where <math>r = |z| = \sqrt{x^2+y^2}</math> and <math>\psi \in [(-\ | + | *Where <math>r = |z| = \sqrt{x^2+y^2}</math> and <math>\psi \in [(-\pi,\pi]</math>. |
*The argument of a complex number is calculated by <math>arg(z)= tan^{-1}(\frac{y}{x}) =\theta</math> in Radians. | *The argument of a complex number is calculated by <math>arg(z)= tan^{-1}(\frac{y}{x}) =\theta</math> in Radians. | ||
*To change the Radian value to Degree we can use DEGREES function or we can multiply the answer with <math>\frac{180}{\pi}</math>. | *To change the Radian value to Degree we can use DEGREES function or we can multiply the answer with <math>\frac{180}{\pi}</math>. | ||
Revision as of 22:26, 17 December 2013
IMARGUMENT(z)
- is the complex number is of the form
- is the order of the Bessel function and is an integer
Description
- This function gives the principal value of the argument of the complex-valued expression .
- i.e The angle from the positive axis to the line segment is called the Argument of a complex number.
- In this function angle value is in Radians.
- Here IMARGUMENT(z), Where is the complex number in the form of . i.e & are the real numbers.
- imaginary unit ..
- An argument of the complex number is any real quantity such that = for some positive real number .
- Where and .
- The argument of a complex number is calculated by in Radians.
- To change the Radian value to Degree we can use DEGREES function or we can multiply the answer with .
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
Examples
- IMARGUMENT("3-2i") = -0.588002604
- IMARGUMENT("5+6i") = 0.876058051
- IMARGUMENT("2") = 0
- IMARGUMENT("4i") = 1.570796327
- DEGREES(IMARGUMENT("2+2i")) = 45
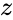 is the complex number is of the form
is the complex number is of the form 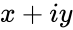
 is the order of the Bessel function and is an integer
is the order of the Bessel function and is an integer &
& 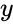 are the real numbers.
are the real numbers.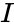 imaginary unit .
imaginary unit .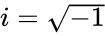 .
.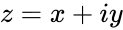 is any real quantity
is any real quantity 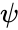 such that
such that 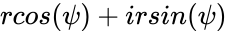 for some positive real number
for some positive real number 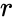 .
.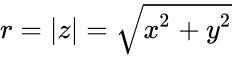 and
and ![{\displaystyle \psi \in [(-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/png/5228fcf0305a61abb4120ee071a752502255a1cb) .
. in Radians.
in Radians.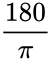 .
.