Difference between revisions of "Manuals/calci/IMPOWER"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*DeMoivre's Theorem is a generalized formula to compute powers of a complex number in it's polar form. | *DeMoivre's Theorem is a generalized formula to compute powers of a complex number in it's polar form. | ||
*i'is the imaginary unit, <math>i=\sqrt{-1}</math> | *i'is the imaginary unit, <math>i=\sqrt{-1}</math> | ||
| − | *Then the power of a complex number is defined by <math>(z)^n=(x+iy)^n=r^n*e^{inθ}=r^n(cosnθ+isinnθ)</math> where <math>r=\sqrt{x^2+y^2}</math>. and <math>θ=tan^-1(y/x)</math>, θ∈ | + | *Then the power of a complex number is defined by <math>(z)^n=(x+iy)^n=r^n*e^{inθ}=r^n(cosnθ+isinnθ)</math> where <math>r=\sqrt{x^2+y^2}</math>. and <math>θ=tan^-1(y/x)</math>, θ∈(-Pi(),Pi()]. |
*This formula is called DeMoivre's theorem of complex numbers. | *This formula is called DeMoivre's theorem of complex numbers. | ||
*We can use COMPLEX function to convert real and imaginary number in to a complex number. | *We can use COMPLEX function to convert real and imaginary number in to a complex number. | ||
Revision as of 21:47, 18 December 2013
IMPOWER(z,n)
- is the complex number is of the form
- is the power value.
Description
- This function gives the value of powers of complex number.
- DeMoivre's Theorem is a generalized formula to compute powers of a complex number in it's polar form.
- i'is the imaginary unit,
- Then the power of a complex number is defined by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (z)^n=(x+iy)^n=r^n*e^{inθ}=r^n(cosnθ+isinnθ)} where . and Failed to parse (syntax error): {\displaystyle θ=tan^-1(y/x)} , θ∈(-Pi(),Pi()].
- This formula is called DeMoivre's theorem of complex numbers.
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
- In IMPOWER(z,n), n can be integer, fractional or negative.
- suppose n is nonnumeric , this function will returns the error value.
Examples
- IMPOWER("4+5i",3)=-235.99999+115i
- IMPOWER("9-7i",4)=-14852-8063.999999i
- IMPOWER("6",9)=10077696(EXCEL)=10077696-8i(CALCI)
- IMPOWER("i",10)=-1-16i(CALCI)=-1+6.1257422745431E-16i
- For imaginary value '0' is not accepting in CALCI.
See Also
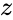 is the complex number is of the form
is the complex number is of the form 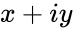
 is the power value.
is the power value.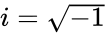
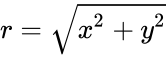 . and Failed to parse (syntax error): {\displaystyle θ=tan^-1(y/x)}
, θ∈(-Pi(),Pi()].
. and Failed to parse (syntax error): {\displaystyle θ=tan^-1(y/x)}
, θ∈(-Pi(),Pi()].