Difference between revisions of "Manuals/calci/IMSQRT"

Revision as of 22:05, 18 December 2013

IMSQRT(z)

This function gives square root of a complex number.
IMSQRT(z), Where z is the complex number is in the form of "x+iy".
where x&y are the real numbers.'i' imaginary unit $i=sqrt(-1)$ .
The square root of a complex number is defined by Failed to parse (syntax error): {\displaystyle \sqrt(z)=\sqrt{x+iy}=\sqrt{r.e^iθ}=sqrt(r)[cos(θ/2)+isin(θ/2)],where r is the modulus of z.<math>r=\sqrt(x^2+y^2)} and θ is the argument of z.Failed to parse (syntax error): {\displaystyle θ=tan^-1(y/x)} also θ∈(-Pi(),Pi()].
We can use COMPLEX function to convert real and imaginary number in to a complex number.

Remarks

Examples

''''''' ''''

Description

This function calculates the square root of a complex number in a + bi or a + bj text format.

IMSQRT

The square root of a complex number is:

IMSQRT(IN)

where IN is the complex number

Let's see an example

I.e =IMSQRT(“2+i”) is 1.4553+0.34356i

@@ Line 1: / Line 1: @@
-<div id="16SpaceContent" align="left"><div class="ZEditBox" align="justify">
+<div style="font-size:30px">'''IMSQRT(z)'''</div><br/>
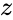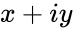
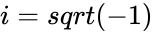+*<math> z </math> is the complex number is of the form <math>x+iy</math>
-Syntax
+==Description==
+*This function gives  square root of a complex number.
+*IMSQRT(z), Where z  is  the complex number is in the form of "x+iy".
+*where x&y are the real numbers.'i' imaginary unit<math>i=sqrt(-1)</math>.
+*The square root of a complex number is defined by <math>\sqrt(z)=\sqrt{x+iy}=\sqrt{r.e^iθ}=sqrt(r)[cos(θ/2)+isin(θ/2)],where r is the modulus of z.<math>r=\sqrt(x^2+y^2)</math> and θ is the argument of z.<math> θ=tan^-1(y/x)</math> also θ∈(-Pi(),Pi()].
+*We can use COMPLEX function to convert real and imaginary number in to a complex number.
 </div></div>
 ----