Difference between revisions of "Manuals/calci/ERFC"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> <font color="#484848"><font face="Arial, sans-serif"><font size="2">'''ERFC(LL'''</font></font></font><font color="#484...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''ERFC(x)'''</div><br/> |
| + | *<math>x</math> is the lower limit. | ||
| − | + | ==Description== | |
| + | *This function gives the complementary ERF function. | ||
| + | *The complementary error function is the error function with the limit x and infinity. It is denoted by erfc(x). | ||
| + | *It is also called scaled complementary error function. | ||
| + | *ERFC is defined by: | ||
| + | <math>ERFC(x)=\frac{2}{\sqrt{\pi}}\int\limits_{x}^{infty}e^{-t^2} dt=1-ERF(x)</math>. | ||
| + | *This function will return the result as error when x is nonnumeric or negative. | ||
| − | + | ==Examples== | |
| − | + | #ERFC(3)=0.0000219610 | |
| − | + | #ERFC(2)=0.0046777624247 | |
| + | #ERFC(0)=1 | ||
| + | #ERFC(-2)=NAN | ||
| − | + | ==See Also== | |
| + | *[[Manuals/calci/ERF | ERF ]] | ||
| − | + | ==References== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 23:26, 25 December 2013
ERFC(x)
- is the lower limit.
Description
- This function gives the complementary ERF function.
- The complementary error function is the error function with the limit x and infinity. It is denoted by erfc(x).
- It is also called scaled complementary error function.
- ERFC is defined by:
.
- This function will return the result as error when x is nonnumeric or negative.
Examples
- ERFC(3)=0.0000219610
- ERFC(2)=0.0046777624247
- ERFC(0)=1
- ERFC(-2)=NAN
 is the lower limit.
is the lower limit.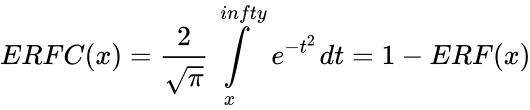 .
.