Difference between revisions of "Manuals/calci/ERFC"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*It is also called scaled complementary error function. | *It is also called scaled complementary error function. | ||
*ERFC is defined by: | *ERFC is defined by: | ||
| − | <math>ERFC(x)=\frac{2}{\sqrt{\pi}}\int\limits_{x}^{infty}e^{-t^2} dt=1-ERF(x)</math>. | + | <math>ERFC(x)=\frac{2}{\sqrt{\pi}}\int\limits_{x}^{\infty}e^{-t^2} dt=1-ERF(x)</math>. |
*This function will return the result as error when x is nonnumeric or negative. | *This function will return the result as error when x is nonnumeric or negative. | ||
Revision as of 23:32, 25 December 2013
ERFC(x)
- is the lower limit.
Description
- This function gives the complementary ERF function.
- The complementary error function is the error function with the limit x and infinity. It is denoted by erfc(x).
- It is also called scaled complementary error function.
- ERFC is defined by:
.
- This function will return the result as error when x is nonnumeric or negative.
Examples
- ERFC(3)=0.0000219610
- ERFC(2)=0.0046777624247
- ERFC(0)=1
- ERFC(-2)=NAN
 is the lower limit.
is the lower limit.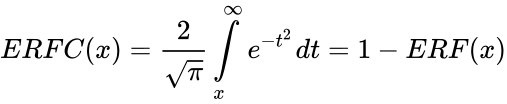 .
.