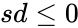Difference between revisions of "Manuals/calci/LOGNORMDIST"
Jump to navigation
Jump to search
| Line 10: | Line 10: | ||
*Suppose <math>x</math> is Normally Distributed function, then <math> y=ln(x)</math> also Normally Distributed | *Suppose <math>x</math> is Normally Distributed function, then <math> y=ln(x)</math> also Normally Distributed | ||
*<math> z=exp(y)</math> also Normally Distributed. | *<math> z=exp(y)</math> also Normally Distributed. | ||
| − | *Let the Normal Distribution function <math>x</math> and its Mean= <math> | + | *Let the Normal Distribution function <math>x</math> and its Mean= <math>\mu</math>, Standard Deviation = <math>\sigma</math> |
*Then the lognormal cumulative distribution is calculated by:<math>F(x,\mu,\sigma)=\frac{1}{2} \left[1+ erf \left (\frac{ln(x)-μ)}{σ\sqrt{2}}\right)\right ]= \phi\left[\frac{ln(x)-\mu}\sigma}\right ]</math> | *Then the lognormal cumulative distribution is calculated by:<math>F(x,\mu,\sigma)=\frac{1}{2} \left[1+ erf \left (\frac{ln(x)-μ)}{σ\sqrt{2}}\right)\right ]= \phi\left[\frac{ln(x)-\mu}\sigma}\right ]</math> | ||
where <math>erf</math> is the error function,. The error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations. | where <math>erf</math> is the error function,. The error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations. | ||
Revision as of 00:17, 31 December 2013
LOGNORMDIST(x,m,sd)
- is the value , is the mean of ,
- And is the standard deviation of .
Description
- This function gives the value of the cumulative log normal distribution.
- This distribution is the continuous probability distribution.
- Lognomal distribution is also called Galton's distribution.
- A random variable which is log-normally distributed takes only positive real values.
- Suppose is Normally Distributed function, then also Normally Distributed
- also Normally Distributed.
- Let the Normal Distribution function and its Mean= , Standard Deviation =
- Then the lognormal cumulative distribution is calculated by:Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x,\mu,\sigma)=\frac{1}{2} \left[1+ erf \left (\frac{ln(x)-μ)}{σ\sqrt{2}}\right)\right ]= \phi\left[\frac{ln(x)-\mu}\sigma}\right ]}
where is the error function,. The error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations.
- And is the Cumulative Distribution function of the Standard Normal distribution.
- This function will give the result as error when
1. Any one of the argument is non-numeric. 2. Suppose or
Examples
- LOGNORMDIST(2,5.4,2.76)=0.044061652
- LOGNORMDIST(10,24.05,12.95)=0.046543186
- LOGNORMDIST(50,87.0036,42.9784)=0.026597569
- LOGNORMDIST(-10,5,2)=NAN
 is the value ,
is the value ,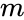 is the mean of
is the mean of 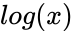 ,
,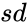 is the standard deviation of
is the standard deviation of 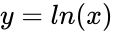 also Normally Distributed
also Normally Distributed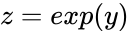 also Normally Distributed.
also Normally Distributed.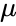 , Standard Deviation =
, Standard Deviation = 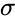
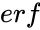 is the error function,. The error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations.
is the error function,. The error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations.
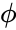 is the Cumulative Distribution function of the Standard Normal distribution.
is the Cumulative Distribution function of the Standard Normal distribution.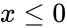 or
or