Difference between revisions of "Manuals/calci/MDETERM"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
*This function gives the determinant value of a matrix. | *This function gives the determinant value of a matrix. | ||
*To calculate the determinant of the matrix we can choose only square matrix. | *To calculate the determinant of the matrix we can choose only square matrix. | ||
| − | *i.e., Number rows and number of columns should be equal.Determinant of the identity matrix is always 1. *Determinant of the matrix A is denoted by det(A) or |A|. | + | *i.e., Number rows and number of columns should be equal. |
| + | *Determinant of the identity matrix is always 1. | ||
| + | *Determinant of the matrix A is denoted by det(A) or |A|. | ||
*Let A be 2x2 matrix with the elements | *Let A be 2x2 matrix with the elements | ||
<math>A = \begin{bmatrix} | <math>A = \begin{bmatrix} | ||
| Line 13: | Line 15: | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
| − | |||
*Then det(A)=ad-bc, where a,b,c,d all are real numbers. | *Then det(A)=ad-bc, where a,b,c,d all are real numbers. | ||
| − | *Let A be the 3x3 matrix with the elements A= | + | *Let A be the 3x3 matrix with the elements |
| − | + | <math>A = \begin{bmatrix} | |
| − | + | a & b & c\\ | |
| + | d & e & f | ||
| + | g & h & i\\ | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
Then |A|=a|e f -b|d f +c|d e | Then |A|=a|e f -b|d f +c|d e | ||
h i| g i| g h| | h i| g i| g h| | ||
Revision as of 03:44, 31 December 2013
MDETERM(arr)
- where is the array of numeric elements
Description
- This function gives the determinant value of a matrix.
- To calculate the determinant of the matrix we can choose only square matrix.
- i.e., Number rows and number of columns should be equal.
- Determinant of the identity matrix is always 1.
- Determinant of the matrix A is denoted by det(A) or |A|.
- Let A be 2x2 matrix with the elements
- Then det(A)=ad-bc, where a,b,c,d all are real numbers.
- Let A be the 3x3 matrix with the elements
Then |A|=a|e f -b|d f +c|d e
h i| g i| g h|
=a(ei-fh) -b(di-fg)+c(dh-eg)
- Let A be a square matrix of order n. Write A = (a_ij),
- Where aij is the entry on the i number of rows and j number of columns and i=1 to n &j=1 to n.
- For any i and j, set Aij (called the cofactors), then the general formula for determinant of the matrix A , |A|=summation (j=1 to n)a_ij A_ij, for any fixed i.
Also|A|=summation (i=1 to n)a_ij A_ij, for any fixed j.
- This function will give the result as error when
1. Any one of the element in array is empty or contain non-numeric 2. Number of rows is not equal to number of columns
Examples
- =MDETERM({6,4,8;3,6,1;2,4,5}) = 104
- =DETERM({-5,10;6,-8}) = -20
- =MDETERM({1,0,2,1;4,0,2,-1;1,4,5,2;3,1,2,0}) = 17
- =MDETERM({1,2,3;5,2,8}) = NAN
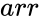 is the array of numeric elements
is the array of numeric elements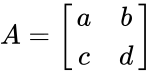
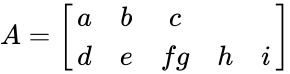 Then |A|=a|e f -b|d f +c|d e
Then |A|=a|e f -b|d f +c|d e