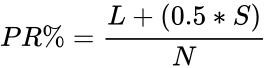Difference between revisions of "Manuals/calci/PERCENTRANK"
Jump to navigation
Jump to search
| Line 8: | Line 8: | ||
*For example, a test score that is greater than or equal to 50% of the scores of people taking the test is said to be at the 50th percentile rank. | *For example, a test score that is greater than or equal to 50% of the scores of people taking the test is said to be at the 50th percentile rank. | ||
*Percentile ranks are commonly used to clarify the interpretation of scores on standardized tests. | *Percentile ranks are commonly used to clarify the interpretation of scores on standardized tests. | ||
| − | * To find the percentile rank of a score is :<math>PR \%= \frac {L+( 0.5*S )}{N} | + | * To find the percentile rank of a score is :<math>PR \%= \frac {L+( 0.5*S )}{N}</math> |
Where, | Where, | ||
L = Number of below rank, | L = Number of below rank, | ||
| Line 15: | Line 15: | ||
*In PERCENTRANK(ar,x),ar is the array of numeric values and x is the value to find the rank. This function gives the result as error when array is empty . | *In PERCENTRANK(ar,x),ar is the array of numeric values and x is the value to find the rank. This function gives the result as error when array is empty . | ||
| − | + | ==Examples== | |
| + | #3 | ||
| + | 4 | ||
| + | 1 | ||
| + | 2 | ||
| + | 1 | ||
| + | PERCENTRANK(A1:A5,2)=0.5 | ||
| + | #7 | ||
| + | 6 | ||
| + | 2 | ||
| + | 5 | ||
| + | 9 | ||
| + | 1 | ||
| + | PERCENTRANK(B1:B6,3)=0.267 | ||
| − | |||
| − | + | ==See Also== | |
| + | *[[Manuals/calci/MAX | MAX ]] | ||
| + | *[[Manuals/calci/MIN | MIN ]] | ||
| + | *[[Manuals/calci/MEDIAN | MEDIAN ]] | ||
| + | *[[Manuals/calci/QUARTILE | QUARTILE ]] | ||
| + | *[[Manuals/calci/PERCENTILE | PERCENTILE ]] | ||
| − | |||
| − | + | ==References== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 00:23, 6 January 2014
PERCENTRANK(ar,x)
- is the array data and is the value
Description
- This function gives the percentage rank of a value in a given set of numbers.
- To calculate the relative standing of a data set we can use this function.
- For example, a test score that is greater than or equal to 50% of the scores of people taking the test is said to be at the 50th percentile rank.
- Percentile ranks are commonly used to clarify the interpretation of scores on standardized tests.
- To find the percentile rank of a score is :
Where, L = Number of below rank, S = Number of same rank, N = Total numbers.
- In PERCENTRANK(ar,x),ar is the array of numeric values and x is the value to find the rank. This function gives the result as error when array is empty .
Examples
- 3
4 1 2 1 PERCENTRANK(A1:A5,2)=0.5
- 7
6 2 5 9 1 PERCENTRANK(B1:B6,3)=0.267
See Also
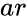 is the array data and
is the array data and  is the value
is the value