Difference between revisions of "Manuals/calci/poisson"
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''POISSON'''(X, Mean, Cumulative) where, '''X''' - are represents number of events. '''Mean '''- is the e...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''POISSON(x,m,cu)'''</div><br/> |
| + | *<math>x</math> is the number of events. | ||
| + | *<math>m </math> is the mean | ||
| + | *<math>cu</math> is the logical value like TRUE or FALSE. | ||
| − | + | ||
| + | ==Description== | ||
| + | *This function gives the value of the Poisson distribution. | ||
| + | *The Poisson distribution is a discrete probability distribution for the counts of events that occur randomly in a given interval of time. | ||
| + | *It is is used to model the number of events occurring within a given time interval. | ||
| + | *In <math>POISSON(x,m,cu), x </math> is the number of events in a given interval of time, <math> m </math> is the Average numeric value and <math> cu </math> is the logical value. | ||
| + | *If it is TRUE, this function will give the cumulative Poisson probability with the number of random events between 0 and x(included). | ||
| + | *If it is FALSE,this function will give the Poisson probability mass function with the number of events occuring will be exactly x. | ||
| + | *The POSSON probability mass function is: <math> f(x,\lambda)=\frac{\lambda^x.e^{-\lambda}}{x!}, x=0,1,2,...where \lambda is the shape parameter and \lambda>0.e is the base of the natural logarithm (e=2.718282). | ||
| + | *The cumulative Poisson probability function is:F(k,λ)=Summation(k=0 to x) e^-λ .λ^k/k!. | ||
| + | *This function will return the result as error when | ||
| + | 1.x or m is nonnumeric. | ||
| + | 2.x<0 or m<0. | ||
where, | where, | ||
| Line 51: | Line 66: | ||
Lets see an example in (Column1, Row1) | Lets see an example in (Column1, Row1) | ||
| − | + | UNIQ1bbe901cd2555324-nowiki-00000004-QINU | |
POISSON returns 0.44568. | POISSON returns 0.44568. | ||
| Line 57: | Line 72: | ||
Cosider an another example | Cosider an another example | ||
| − | + | UNIQ1bbe901cd2555324-nowiki-00000005-QINU | |
POISSON returns 0.195367. | POISSON returns 0.195367. | ||
Revision as of 02:15, 6 January 2014
- is the number of events.
- is the mean
- is the logical value like TRUE or FALSE.
Description
- This function gives the value of the Poisson distribution.
- The Poisson distribution is a discrete probability distribution for the counts of events that occur randomly in a given interval of time.
- It is is used to model the number of events occurring within a given time interval.
- In is the number of events in a given interval of time, is the Average numeric value and is the logical value.
- If it is TRUE, this function will give the cumulative Poisson probability with the number of random events between 0 and x(included).
- If it is FALSE,this function will give the Poisson probability mass function with the number of events occuring will be exactly x.
- The POSSON probability mass function is: <math> f(x,\lambda)=\frac{\lambda^x.e^{-\lambda}}{x!}, x=0,1,2,...where \lambda is the shape parameter and \lambda>0.e is the base of the natural logarithm (e=2.718282).
- The cumulative Poisson probability function is:F(k,λ)=Summation(k=0 to x) e^-λ .λ^k/k!.
- This function will return the result as error when
1.x or m is nonnumeric. 2.x<0 or m<0.
where,
X - are represents number of events.
Mean - is the expected numeric values.
Cumulative - returned the logical value that determines the form of the probability distribution.
If TRUE - returnd the cumulative Poisson probability that the number of random events occuring will be between 0 and X.
If FALSE -returns the Poisson probability mass function that the number of events occuring will be exactly X.
Returns the Poisson distribution.
Formula :-
If Cumulative =FALSE
POISSON = (e-λ λ× ) / x!
If Cumulative = TRUE
POISSON = Σ(e-λ λ× ) /k!
If X orMean is nonnumeric, POISSON returns the #ERROR.
If X < 0 or Mean < 0 ,POISSON returns the #ERROR.
POISSON
Lets see an example in (Column1, Row1)
?UNIQ1bbe901cd2555324-nowiki-00000004-QINU?
POISSON returns 0.44568.
Cosider an another example
?UNIQ1bbe901cd2555324-nowiki-00000005-QINU?
POISSON returns 0.195367.
| Column1 | Column2 | Column3 | Column4 | |
| Row1 | 0.44568 | |||
| Row2 | 0.195367 | |||
| Row3 | ||||
| Row4 | ||||
| Row5 | ||||
| Row6 |
 is the number of events.
is the number of events. is the mean
is the mean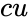 is the logical value like TRUE or FALSE.
is the logical value like TRUE or FALSE.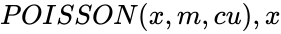 is the number of events in a given interval of time,
is the number of events in a given interval of time,