Difference between revisions of "Manuals/calci/PERCENTRANK"
Jump to navigation
Jump to search
| Line 10: | Line 10: | ||
* To find the percentile rank of a score is :<math>PR \%= \frac {L+( 0.5*S )}{N}</math> | * To find the percentile rank of a score is :<math>PR \%= \frac {L+( 0.5*S )}{N}</math> | ||
Where, | Where, | ||
| − | L = Number of below rank, | + | <math>L</math> = Number of below rank, |
| − | S = Number of same rank, | + | <math>S</math> = Number of same rank, |
| − | N = Total numbers. | + | <math>N</math> = Total numbers. |
| − | *In PERCENTRANK(ar,x),ar is the array of numeric values and x is the value to find the rank. This function gives the result as error when array is empty . | + | *In <math>PERCENTRANK(ar,x)</math>, <math>ar</math> is the array of numeric values and <math>x</math> is the value to find the rank. |
| + | *This function gives the result as error when array is empty . | ||
==Examples== | ==Examples== | ||
Revision as of 02:54, 7 January 2014
PERCENTRANK(ar,x)
- is the array data and is the value
Description
- This function gives the percentage rank of a value in a given set of numbers.
- To calculate the relative standing of a data set we can use this function.
- For example, a test score that is greater than or equal to 50% of the scores of people taking the test is said to be at the 50th percentile rank.
- Percentile ranks are commonly used to clarify the interpretation of scores on standardized tests.
- To find the percentile rank of a score is :
Where, = Number of below rank, = Number of same rank, = Total numbers.
- In , is the array of numeric values and is the value to find the rank.
- This function gives the result as error when array is empty .
Examples
- 3
4 1 2 1 PERCENTRANK(A1:A5,2)=0.5
- 7
6 2 5 9 1 PERCENTRANK(B1:B6,3)=0.267
See Also
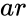 is the array data and
is the array data and  is the value
is the value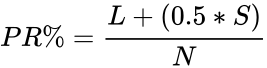
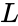 = Number of below rank,
= Number of below rank,
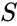 = Number of same rank,
= Number of same rank,
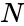 = Total numbers.
= Total numbers.
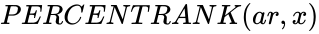 ,
,