Difference between revisions of "Manuals/calci/poisson"
Jump to navigation
Jump to search
| Line 3: | Line 3: | ||
*<math>m </math> is the mean | *<math>m </math> is the mean | ||
*<math>cu</math> is the logical value like TRUE or FALSE. | *<math>cu</math> is the logical value like TRUE or FALSE. | ||
| − | |||
==Description== | ==Description== | ||
| Line 11: | Line 10: | ||
*In <math>POISSON(x,m,cu), x </math> is the number of events in a given interval of time, <math> m </math> is the Average numeric value and <math> cu </math> is the logical value. | *In <math>POISSON(x,m,cu), x </math> is the number of events in a given interval of time, <math> m </math> is the Average numeric value and <math> cu </math> is the logical value. | ||
*If it is TRUE, this function will give the cumulative Poisson probability with the number of random events between 0 and x(included). | *If it is TRUE, this function will give the cumulative Poisson probability with the number of random events between 0 and x(included). | ||
| − | *If it is FALSE,this function will give the Poisson probability mass function with the number of events | + | *If it is FALSE,this function will give the Poisson probability mass function with the number of events occurring will be exactly x. |
| − | *The <math>POISSON </math>probability mass function is: <math> f(x,\lambda)=\frac{\lambda^x.e^{-\lambda}}{x!}</math>, | + | *The <math>POISSON </math>probability mass function is: <math> f(x,\lambda)=\frac{\lambda^x.e^{-\lambda}}{x!}</math>, <math>x=0,1,2,...where <math> \lambda </math> is the shape parameter and <math>\lambda</math>>0. <math>e</math> is the base of the natural logarithm (e=2.718282). |
*The cumulative Poisson probability function is:<math>F(k,\lambda)=\sum_{k=0}^x \frac{e^{-\lambda} .\lambda^k}{k!}</math>. | *The cumulative Poisson probability function is:<math>F(k,\lambda)=\sum_{k=0}^x \frac{e^{-\lambda} .\lambda^k}{k!}</math>. | ||
*This function will return the result as error when | *This function will return the result as error when | ||
| − | 1.x or m is | + | 1.<math>x</math> or <math>m<math> is non-numeric. |
| − | 2.x<0 or m<0. | + | 2.<math>x<0</math> or <math>m<0</math>. |
==Examples== | ==Examples== | ||
| Line 27: | Line 26: | ||
==See Also== | ==See Also== | ||
*[[Manuals/calci/EXPONDIST | EXPONDIST ]] | *[[Manuals/calci/EXPONDIST | EXPONDIST ]] | ||
| − | |||
==References== | ==References== | ||
| + | [http://en.wikipedia.org/wiki/Poisson_distribution Poisson distribution ] | ||
Revision as of 03:25, 7 January 2014
POISSON(x,m,cu)
- is the number of events.
- is the mean
- is the logical value like TRUE or FALSE.
Description
- This function gives the value of the Poisson distribution.
- The Poisson distribution is a discrete probability distribution for the counts of events that occur randomly in a given interval of time.
- It is is used to model the number of events occurring within a given time interval.
- In is the number of events in a given interval of time, is the Average numeric value and is the logical value.
- If it is TRUE, this function will give the cumulative Poisson probability with the number of random events between 0 and x(included).
- If it is FALSE,this function will give the Poisson probability mass function with the number of events occurring will be exactly x.
- The probability mass function is: , is the shape parameter and >0. is the base of the natural logarithm (e=2.718282).
- The cumulative Poisson probability function is:.
- This function will return the result as error when
1. or or .
Examples
- POISSON(6,2,TRUE)=0.995466194
- POISSON(6,2,FALSE)=0.012029803
- POISSON(10.2,7,TRUE)=0.901479206
- POISSON(10.2,7,FALSE)=0.070983269
- POISSON(6,0,TRUE)=1
 is the number of events.
is the number of events. is the mean
is the mean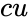 is the logical value like TRUE or FALSE.
is the logical value like TRUE or FALSE.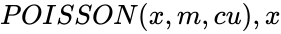 is the number of events in a given interval of time,
is the number of events in a given interval of time, 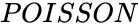 probability mass function is:
probability mass function is:  ,
, 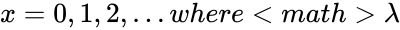 is the shape parameter and
is the shape parameter and 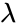 >0.
>0. 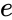 is the base of the natural logarithm (e=2.718282).
is the base of the natural logarithm (e=2.718282).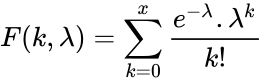 .
.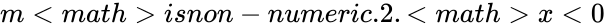 or
or  .
.