Difference between revisions of "Manuals/calci/FORECAST"
Jump to navigation
Jump to search
| Line 8: | Line 8: | ||
*This function gives the predicted value of the dependent variable for the specific value, x, of the independent variable by using a least squares linear regression to predict y values from x values. | *This function gives the predicted value of the dependent variable for the specific value, x, of the independent variable by using a least squares linear regression to predict y values from x values. | ||
*In <math>FORECAST(n,y,x), n</math> is the data point to predict a value. <math>y</math> is the dependent array of data to predict the <math>y</math>-value and <math>x</math> is the independent array of data to predict the <math>y</math>-value. | *In <math>FORECAST(n,y,x), n</math> is the data point to predict a value. <math>y</math> is the dependent array of data to predict the <math>y</math>-value and <math>x</math> is the independent array of data to predict the <math>y</math>-value. | ||
| − | *The formula for <math>FORECAST</math> is <math> a+bx</math> , where <math>a=\bar{y}-b \bar{x} and b= | + | *The formula for <math>FORECAST</math> is <math> a+bx</math> , where <math>a=\bar{y}-b \bar{x} and b=\frac{\sum (x-\bar{x})(y-\bar{y}}{\sum(x-\bar{x})^2}</math>. Here <math>\bar{x}</math> and <math>\bar{y}</math> are the sample means of x and y. |
| − | 2. The values of x and y are empty or contain a different number of data points. | + | *This function will give the result as error when |
| − | 3. The variance of x is zero. | + | 1. Any one of the value is nonnumeric. |
| + | 2. The values of x and y are empty or contain a different number of data points. | ||
| + | 3. The variance of x is zero. | ||
where n, y and x . | where n, y and x . | ||
Revision as of 05:20, 14 January 2014
FORECAST(n,y,x)
- is the data point .
- is the dependent array of data.
- is the independent array of data.
Description
- This function gives the predicted value of the dependent variable for the specific value, x, of the independent variable by using a least squares linear regression to predict y values from x values.
- In is the data point to predict a value. is the dependent array of data to predict the -value and is the independent array of data to predict the -value.
- The formula for is , where . Here and are the sample means of x and y.
- This function will give the result as error when
1. Any one of the value is nonnumeric. 2. The values of x and y are empty or contain a different number of data points. 3. The variance of x is zero. where n, y and x .
FORECAST(x1, ky1’s, kx1’s)
Where X1 is the data point, ky1 is the dependent array or range of data and ky2
is the independent array or range of data.
It Predicts or calculates a future value by using existing values. The predicted value is a y1-value for a given x1-value.
· FORECAST displays an error, when x is nonnumeric.
· when the variance of kx1’s equals zero FORECAST displays errror.
· The equation for FORECAST is a+bx, where:
and:
and where x and y are the sample means AVERAGE(kx1's) and AVERAGE(ky1's).
FORECAST
Syntax
Remarks
Examples
Description
| Column1 | Column2 | Column3 | Column4 | |
| Row1 | 4 | 25 | 4.730174 | |
| Row2 | 5 | 23 | ||
| Row3 | 8 | 32 | ||
| Row4 | 17 | 36 | ||
| Row5 | 22 | 40 | 0 | |
| Row6 |
AVEDEV (N1, N2...) Where N1, N 2 ... are positive integers.
?UNIQee1806e3b9c8b1d6-nowiki-00000002-QINU?
 is the data point .
is the data point .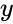 is the dependent array of data.
is the dependent array of data. is the independent array of data.
is the independent array of data.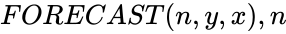 is the data point to predict a value.
is the data point to predict a value.  is
is 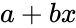 , where
, where 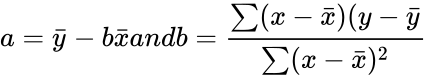 . Here
. Here 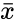 and
and 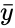 are the sample means of x and y.
are the sample means of x and y.