Difference between revisions of "Manuals/calci/GROWTH"
Jump to navigation
Jump to search
| Line 23: | Line 23: | ||
==Examples== | ==Examples== | ||
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
| Line 37: | Line 36: | ||
|} | |} | ||
| − | #GROWTH( | + | #GROWTH(A1:E1,A2:E2) = 1.0000000039046144 |
| + | |||
| + | |||
| + | ==See Also== | ||
| + | |||
| + | |||
| + | ==References== | ||
Revision as of 02:52, 15 January 2014
GROWTH(y,x,x1,c)
- is the set of y values.
- is the set of x values.
- is the new x value.
- is the constant value.
Description
- This function calculates an exponential trend of the values for new values by using given and values.
- Growth rate is a financial term used to describe a method of projecting the rate of return on a given investment over a period of time.
- In is the set of values used to predict the exponential growth, is the set of values used to predict the exponential growth,
- is the set of new x-values, for which the function calculates corresponding new y-values and is the constant. It is either a TRUE or FALSE.
- When value is TRUE, then the constant value is calculated normally. When value is FALSE, then the constant is set to 1.
- Here value is required. and is optional.
- If value is omitted, then it is assumed to be the array{1,2,3..} which is the same size of .
- If value is omitted, then it is assumed to be the same size of .
- If both and are omitted, then they are assumed to be the array {1,2,3..} which is the same size of .
- Also and values is the set of values with the relationship .
- When entering an array constant for an argument such as , use commas to separate values in the same row and semicolons to separate rows.
- This function will return the result as error when any one of the value in value is 0 or negative.
Examples
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 2001 | 2002 | 2003 | 2004 | 2005 |
| 2 | 1000000 | 1100000 | 1252000 | 1375000 | 1500000 |
- GROWTH(A1:E1,A2:E2) = 1.0000000039046144
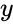 is the set of y values.
is the set of y values. is the set of x values.
is the set of x values.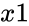 is the new x value.
is the new x value.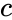 is the constant value.
is the constant value.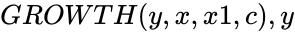 is the set of
is the set of 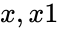 and
and 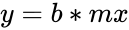 .
.