Difference between revisions of "Manuals/calci/SERIESSUM"
Jump to navigation
Jump to search
| Line 15: | Line 15: | ||
==Examples== | ==Examples== | ||
| − | #SERIESSUM(3,2,2,{1,2,3,4,5,6}) = 3512493 | + | #=SERIESSUM(3,2,2,{1,2,3,4,5,6}) = 3512493 |
| − | #SERIESSUM(1,0,4,{1,2,3}) = 6 | + | #=SERIESSUM(1,0,4,{1,2,3}) = 6 |
| − | #SERIESSUM(2,1,5,{2,4,6,8}) = 536836 | + | #=SERIESSUM(2,1,5,{2,4,6,8}) = 536836 |
| − | #SERIESSUM(0,2,4,{1,2,3,4,5}) = 0 | + | #=SERIESSUM(0,2,4,{1,2,3,4,5}) = 0 |
| − | #SERIESSUM(1,0,3,{1,2,3,4,5}) = 15 | + | #=SERIESSUM(1,0,3,{1,2,3,4,5}) = 15 |
| − | + | #=SERIESSUM(1,1,5,{1}) = 1 | |
==See Also== | ==See Also== | ||
Revision as of 03:19, 16 January 2014
SERIESSUM(x,n,m,k)
- is the power series value.
- is the initial power value.
- is the step value to increase the n value for each term.
- is the set of coefficients by which each successive power of x is multiplied.
Description
- This function gives the value of the seriessum of the given set of values.
- Seriessum is defined by the following formulaFailed to parse (syntax error): {\displaystyle :SERIESSUM(x,n,m,a)= a_1x^n + a_2x^{(n+m)} + a_3x^{(n+2m)} + … + a_jx^{(n+(j-1)m)} } .
- Here is the powerseries value, is the starting power value, is the increasing value of a power and is the set of coefficients.
- According to the number of coefficients , the number of terms of the power series also get varies.
- For example there 5 values in coefficients, then 5 terms will be there in power series.
This function will give the result as error when any one of the argument is nonnumeric.
Examples
- =SERIESSUM(3,2,2,{1,2,3,4,5,6}) = 3512493
- =SERIESSUM(1,0,4,{1,2,3}) = 6
- =SERIESSUM(2,1,5,{2,4,6,8}) = 536836
- =SERIESSUM(0,2,4,{1,2,3,4,5}) = 0
- =SERIESSUM(1,0,3,{1,2,3,4,5}) = 15
- =SERIESSUM(1,1,5,{1}) = 1
 is the power series value.
is the power series value. is the initial power value.
is the initial power value.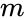 is the step value to increase the n value for each term.
is the step value to increase the n value for each term.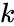 is the set of coefficients by which each successive power of x is multiplied.
is the set of coefficients by which each successive power of x is multiplied. is the set of coefficients.
is the set of coefficients.