Difference between revisions of "Manuals/calci/RSQ"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> <font face="Arial, sans-serif"><font size="2">'''RSQ'''</font></font><font face="Arial, sans-serif"><font size="2">(</f...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''RSQ(ar1,ar2)'''</div><br/> |
| + | *<math>ar1</math> is the array of y values . | ||
| + | *<math>ar2</math> is the array of x values. | ||
| − | |||
| − | </ | + | ==Description== |
| − | ---- | + | *This function gives the square of Pearson Product Moment Correlation Coefficient. |
| − | < | + | *This function is calculated using the data points of <math>y</math> and <math>x</math> values. |
| − | + | *The formula for PPMC,<math>r</math> is defined by: | |
| − | + | <math> r= \frac{ \Sigma(x-\bar{x})(y-\bar{y})}{\sqrt {\Sigma(x-\bar{x})^2(y-\bar{y})^2}}</math> | |
| + | where <math> \bar{x}</math> and <math>\bar{y} </math> are Average of the two Samples <math>x </math> and <math>y </math>. | ||
| + | *This function gives the value of r^2, which is the square of this correlation coefficient. | ||
| + | *The square value can be interpreted as the proportion of the variance in y attributable to the variance in x. | ||
| + | *In <math> RSQ(ar1,ar2)</math>,the value of <math>ar1</math> and <math>ar1</math> must be either numbers or names, array,constants or references that contain numbers. | ||
| + | *Suppose the array contains text,logicl values or empty cells, like that values are not considered. | ||
| + | *This function will return the result as error when 1. ar1 and ar2 are empty or having the different number of data points. | ||
| + | 2. The arguments having only one data point. | ||
| + | 3. The arguments that are error values or text that cannot be translated in to numbers. | ||
| + | We want to know more detail, see PEARSON. | ||
| − | |||
| − | + | ==Examples== | |
| − | + | {| class="wikitable" | |
| − | + | |+Spreadsheet | |
| − | + | |- | |
| − | + | ! !! A !! B !! C !!D !! E !! F !! G !! H | |
| − | + | |- | |
| − | + | ! 1 | |
| − | + | | 12 || 10 || 17 || 21 || 25 || 31 || 19 || 5 | |
| − | + | |- | |
| − | + | ! 2 | |
| − | + | | 4 || 37 || 8 || 18 || 0 || 13 || 15 || 41 | |
| − | + | |- | |
| − | + | ! 3 | |
| − | + | | 9 || | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | {| | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |- | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |- | ||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | | | ||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |- | ||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 03:35, 16 January 2014
RSQ(ar1,ar2)
- is the array of y values .
- is the array of x values.
Description
- This function gives the square of Pearson Product Moment Correlation Coefficient.
- This function is calculated using the data points of and values.
- The formula for PPMC, is defined by:
where and are Average of the two Samples and .
- This function gives the value of r^2, which is the square of this correlation coefficient.
- The square value can be interpreted as the proportion of the variance in y attributable to the variance in x.
- In ,the value of and must be either numbers or names, array,constants or references that contain numbers.
- Suppose the array contains text,logicl values or empty cells, like that values are not considered.
- This function will return the result as error when 1. ar1 and ar2 are empty or having the different number of data points.
2. The arguments having only one data point. 3. The arguments that are error values or text that cannot be translated in to numbers. We want to know more detail, see PEARSON.
Examples
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| 1 | 12 | 10 | 17 | 21 | 25 | 31 | 19 | 5 |
| 2 | 4 | 37 | 8 | 18 | 0 | 13 | 15 | 41 |
| 3 | 9 |
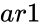 is the array of y values .
is the array of y values .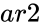 is the array of x values.
is the array of x values.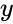 and
and  values.
values. is defined by:
is defined by: where
where 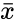 and
and 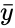 are Average of the two Samples
are Average of the two Samples 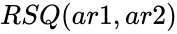 ,the value of
,the value of