Difference between revisions of "Manuals/calci/STEYX"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> <font color="#484848"><font face="Arial, sans-serif"><font size="2">'''STEYX'''</font></font></font><font color="#48484...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''STEYX(y,x)'''</div><br/> |
| − | + | *<math>y</math> is set of dependent values. | |
| − | + | *<math>x </math> is the set of independent values. | |
| − | |||
| − | |||
| − | |||
| − | * < | + | ==Description== |
| − | * < | + | *This function gives the standard error of the regression, which also is known as the standard error of the estimate. |
| + | *It is calculates the standard error for the straight line of best fit through a supplied set of <math> x </math> and <math> y </math> values. | ||
| + | *The standard error for this line provides a measure of the error in the prediction of <math> y </math> for an individual <math> x </math>. | ||
| + | *The equation for the standard error of the predicted <math> y </math> is: SQRT(1/(n-2)[summation (y-y(bar)^2-[summation (x-x(bar)(y-y(bar)]^2/summation(x-x(bar))^2] ,where x(bar) and y(bar) are the sample mean <math> x </math> and <math> y </math>. | ||
| + | *In <math> STEYX(y,x), y </math> is the array of the numeric dependent values and <math> x </math> is the array of the independent values. | ||
| + | *The arguments can be be either numbers or names, array,constants or references that contain numbers. | ||
| + | *Suppose the array contains text,logical values or empty cells, like that values are not considered. | ||
| + | *This function will return the result as error when | ||
| + | 1. Any one of the argument is nonnumeric. | ||
| + | 2. x and y are empty or that have less than three data points. | ||
| + | 3. x and y have a different number of data points. | ||
| − | |||
| − | + | ==Examples== | |
| − | + | 1.y={6,8,10,13,15,5} | |
| − | + | x={1,4,9,11,20,3} | |
| + | STEYX(G1:G6,H1:H6)=1.4350701130 | ||
| + | 2.y={2,9,1,8,17} | ||
| + | x={10,4,11,2,6} | ||
| + | STEYX(A1:A5,B1:B5)=5.944184833375 | ||
| + | 3.y={1,2,4,5,8} | ||
| + | x={10,4,7,5} | ||
| + | STEYX(A1:A5,B1:B4)=NAN | ||
| − | + | ==See Also== | |
| + | *[[Manuals/calci/INTERCEPT | INTERCEPT]] | ||
| + | *[[Manuals/calci/LINEST | LINEST ]] | ||
| + | *[[Manuals/calci/PEARSON | PEARSON ]] | ||
| − | |||
| − | |||
| − | |||
| − | + | ==References== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 03:22, 20 January 2014
STEYX(y,x)
- is set of dependent values.
- is the set of independent values.
Description
- This function gives the standard error of the regression, which also is known as the standard error of the estimate.
- It is calculates the standard error for the straight line of best fit through a supplied set of and values.
- The standard error for this line provides a measure of the error in the prediction of for an individual .
- The equation for the standard error of the predicted is: SQRT(1/(n-2)[summation (y-y(bar)^2-[summation (x-x(bar)(y-y(bar)]^2/summation(x-x(bar))^2] ,where x(bar) and y(bar) are the sample mean and .
- In is the array of the numeric dependent values and is the array of the independent values.
- The arguments can be be either numbers or names, array,constants or references that contain numbers.
- Suppose the array contains text,logical values or empty cells, like that values are not considered.
- This function will return the result as error when
1. Any one of the argument is nonnumeric. 2. x and y are empty or that have less than three data points. 3. x and y have a different number of data points.
Examples
1.y={6,8,10,13,15,5}
x={1,4,9,11,20,3}
STEYX(G1:G6,H1:H6)=1.4350701130 2.y={2,9,1,8,17} x={10,4,11,2,6} STEYX(A1:A5,B1:B5)=5.944184833375 3.y={1,2,4,5,8} x={10,4,7,5} STEYX(A1:A5,B1:B4)=NAN
See Also
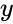 is set of dependent values.
is set of dependent values. is the set of independent values.
is the set of independent values.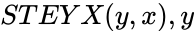 is the array of the numeric dependent values and
is the array of the numeric dependent values and