Difference between revisions of "Manuals/calci/REGRESSION"
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''REGRESSIONANALYSIS'''(XRange, YRange, ConfidenceLevel, NewTableFlag) where, '''XRange '''- Input range sho...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''REGRESSIONANALYSIS(y,x)'''</div><br/> |
| + | *<math>y </math> is the set of dependent variables . | ||
| + | *<math>x </math> is the set of independent variables. | ||
| + | |||
| + | ==Description== | ||
| + | *This function is calculating the Regression analysis of the given data. | ||
| + | *This analysis is very useful for the analyzation of large amounts of data and making predictions. | ||
| + | *This analysis give the result in three table values. | ||
| + | # Regression statistics table. | ||
| + | # ANOVA table. | ||
| + | # Residual output. | ||
| + | *1.Regression statistics : | ||
| + | *It contains multiple R, R Square, Adjusted R Square, Standard Error and observations. | ||
| + | *R square gives the fittness of the data with the regression line. | ||
| + | *That value is closer to 1 is the better the regression line fits the data. | ||
| + | *Standard Error refers to the estimated standard deviation of the error term. It is called the standard error of the regression. | ||
| + | *2.ANOVA table: | ||
| + | *ANOVA is the analysis of variance. | ||
| + | *This table splits in to two components which is Residual and Regression. | ||
| + | *Total sum of squares= Residual (error) sum of squares+ Regression (explained) sum of squares. | ||
| + | *Also this table gives the probability, T stat, significance of F and P. | ||
| + | *When the significance of F is < 0.05, then the result for the given data is statistically significant. | ||
| + | *When the significance of F is > 0.05, then better to stop using this set of independent variables. | ||
| + | *Then remove a variable with a high P-value and returnun the regression until Significance F drops below 0.05. | ||
| + | *So the Significance of P value should be <0.05. | ||
| + | *This table containing the regression coefficient values also. | ||
| + | *3.Residual output: | ||
| + | *The residuals show you how far away the actual data points are fom the predicted data points. | ||
| + | |||
| + | |||
| + | ==Examples== | ||
| + | #Temperature - Drying time(hours) | ||
| + | 54 8 | ||
| + | 63 6 | ||
| + | 75 3 | ||
| + | 82 1 | ||
| + | =REGRESSIONANALYSIS(A1:A4,B1:B4)= | ||
| + | Unit sales Ads population | ||
| + | 4000 12000 300000 | ||
| + | 5200 13150 411000 | ||
| + | 6800 14090 500000 | ||
| + | 8000 11900 650000 | ||
| + | 10000 15000 800000 | ||
| + | |||
| + | |||
| + | where and x | ||
'''REGRESSIONANALYSIS'''(XRange, YRange, ConfidenceLevel, NewTableFlag) | '''REGRESSIONANALYSIS'''(XRange, YRange, ConfidenceLevel, NewTableFlag) | ||
| Line 21: | Line 66: | ||
Lets see an example in (Column3Row1) | Lets see an example in (Column3Row1) | ||
| − | + | UNIQad0c61c6a857529e-nowiki-00000004-QINU | |
REGRESSIONANALYSIS returns the result in new sheet(5Space). | REGRESSIONANALYSIS returns the result in new sheet(5Space). | ||
| − | + | UNIQad0c61c6a857529e-nowiki-00000005-QINU | |
RANKANDPERCENTILE returns the #ERROR(ConfidenceLevel=-5). | RANKANDPERCENTILE returns the #ERROR(ConfidenceLevel=-5). | ||
Revision as of 09:38, 20 January 2014
- is the set of dependent variables .
- is the set of independent variables.
Description
- This function is calculating the Regression analysis of the given data.
- This analysis is very useful for the analyzation of large amounts of data and making predictions.
- This analysis give the result in three table values.
- Regression statistics table.
- ANOVA table.
- Residual output.
- 1.Regression statistics :
- It contains multiple R, R Square, Adjusted R Square, Standard Error and observations.
- R square gives the fittness of the data with the regression line.
- That value is closer to 1 is the better the regression line fits the data.
- Standard Error refers to the estimated standard deviation of the error term. It is called the standard error of the regression.
- 2.ANOVA table:
- ANOVA is the analysis of variance.
- This table splits in to two components which is Residual and Regression.
- Total sum of squares= Residual (error) sum of squares+ Regression (explained) sum of squares.
- Also this table gives the probability, T stat, significance of F and P.
- When the significance of F is < 0.05, then the result for the given data is statistically significant.
- When the significance of F is > 0.05, then better to stop using this set of independent variables.
- Then remove a variable with a high P-value and returnun the regression until Significance F drops below 0.05.
- So the Significance of P value should be <0.05.
- This table containing the regression coefficient values also.
- 3.Residual output:
- The residuals show you how far away the actual data points are fom the predicted data points.
Examples
- Temperature - Drying time(hours)
54 8 63 6 75 3 82 1
REGRESSIONANALYSIS(A1:A4,B1:B4)
Unit sales Ads population 4000 12000 300000 5200 13150 411000 6800 14090 500000 8000 11900 650000 10000 15000 800000
where and x
REGRESSIONANALYSIS(XRange, YRange, ConfidenceLevel, NewTableFlag)
where,
XRange - Input range should be one block.
YRange - Input range should be one block.
ConfidenceLevel - represents the confidence level for percentage nad value should in between 0 and 100.the default percentage is 95.
NewTableFlag - is the TRUE or FALSE.If set as TRUE,the result in new sheet. If NewTableFlag is omitted, it assumed to be FALSE.
Lets see an example in (Column3Row1)
?UNIQad0c61c6a857529e-nowiki-00000004-QINU?
REGRESSIONANALYSIS returns the result in new sheet(5Space).
?UNIQad0c61c6a857529e-nowiki-00000005-QINU?
RANKANDPERCENTILE returns the #ERROR(ConfidenceLevel=-5).
REGRESSION
If ConfidenceLevel < 0 or ConfidenceLevel >100, REGRESSIONANALYSIS returns the #ERROR.
If Lengthof XRange != Lengthof YRange, it returns the #ERROR.
| Column1 | Column2 | Column3 | Column4 | |
| Row1 | 1 | 3 | 5Space | |
| Row2 | 7 | 8 | ||
| Row3 | 12 | 10 | ||
| Row4 | 17 | 18 | #ERROR | |
| Row5 | 37 | 36 | ||
| Row6 | 6 | 5 |
| Regression | Statistics |
|---|---|
| Multiple R | 0.9933541399262806 |
| R Square | 0.9867524473086807 |
| AdjustedRSquare | 0.9834405591358509 |
| StandardError | 1.6492920155683643 |
| Observations | 6 |
| Source of Variation | Sum of Squares | Degree of Freedom | Mean of Squares | F | Significance F |
|---|---|---|---|---|---|
| Regression: | 810.452676722863 | 1 | 810.452676722863 | 297.9425620115529 | 0.0000661044188125954 |
| Residual: | 10.880656610470271 | 4 | 2.720164152617568 | ||
| Total: | 821.3333333333333 | 5 |
| Coefficients | Standard Error | T Statistics | Probability | Lower 95% | Upper 95% | Lower95% | Upper95% | |
|---|---|---|---|---|---|---|---|---|
| Intercept | -0.5146406388642397 | 1.0473758171565741 | -0.4913619642865071 | 0.6489114785470887 | -3.4226220244213423 | 2.393340746692863 | -3.422622024421344 | 2.3933407466928646 |
| X Variable | 1.038598047914818 | 0.06017016854489271 | 17.26101277479262 | 0.00006610441881260698 | 0.8715388823047108 | 1.2056572135249252 | 0.8715388823047107 | 1.2056572135249252 |
| Observation | Predicted Y | Residuals | Standard Residuals |
|---|---|---|---|
| 1 | 2.601153504880214 | -1.6011535048802141 | -1.0854015072917171 |
| 2 | 7.7941437444543045 | -0.7941437444543045 | -0.5383398997096632 |
| 3 | 9.871339840283941 | 2.128660159716059 | 1.4429915300597537 |
| 4 | 18.180124223602483 | -1.1801242236024833 | -0.7999911358813972 |
| 5 | 36.8748890860692 | 0.1251109139307971 | 0.08481109034532615 |
| 6 | 4.678349600709851 | 1.3216503992901493 | 0.8959299224777 |
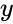 is the set of dependent variables .
is the set of dependent variables . is the set of independent variables.
is the set of independent variables.