Difference between revisions of "Manuals/calci/PEARSON"
Jump to navigation
Jump to search
| Line 12: | Line 12: | ||
0 indicates no correlation | 0 indicates no correlation | ||
-1 indicates the perfect negative correlation. | -1 indicates the perfect negative correlation. | ||
| − | *The formula for PPMC,<math> r </math> is defined by: | + | *The formula for PPMC, <math> r </math> is defined by: |
<math> r= \frac{ \Sigma(x-\bar{x})(y-\bar{y})}{\sqrt {\Sigma(x-\bar{x})^2(y-\bar{y})^2}}</math> | <math> r= \frac{ \Sigma(x-\bar{x})(y-\bar{y})}{\sqrt {\Sigma(x-\bar{x})^2(y-\bar{y})^2}}</math> | ||
where <math> \bar{x}</math> and <math>\bar{y} </math> are Average of the two Samples <math>x </math> and <math>y </math>. | where <math> \bar{x}</math> and <math>\bar{y} </math> are Average of the two Samples <math>x </math> and <math>y </math>. | ||
| − | *In <math>PEARSON( | + | *In <math>PEARSON(ar_1,ar_2)</math>, the value of <math> ar_1</math> and <math> ar_2</math> must be either numbers or names, array,constants or references that contain numbers. |
| − | *Suppose the array contains text,logicl values or empty cells, like that values are not considered. | + | *Suppose the array contains text, logicl values or empty cells, like that values are not considered. |
| − | *This function will return the result as error when the number of values are different for <math> | + | *This function will return the result as error when the number of values are different for <math> ar_1 </math> and <math> ar_2 </math>. |
==Examples== | ==Examples== | ||
Revision as of 02:01, 22 January 2014
PEARSON (ar1,ar2)
- is the array of independent values
- is the array of dependent values.
Description
- This function gives the Pearson Product-Moment Correlation Coefficient.
- It is denoted by PPMC, which shows the linear relationship between two variables.
- It is a measure of the strength of a linear association between two variables .
- The two variables and , giving a value between +1 and −1 inclusive.
- Here
+1 indicates the perfect positive correlation, 0 indicates no correlation -1 indicates the perfect negative correlation.
- The formula for PPMC, is defined by:
where and are Average of the two Samples and .
- In , the value of and must be either numbers or names, array,constants or references that contain numbers.
- Suppose the array contains text, logicl values or empty cells, like that values are not considered.
- This function will return the result as error when the number of values are different for and .
Examples
| A | B | C | |
|---|---|---|---|
| 1 | 5 | 9 | 10 |
| 2 | 8 | 12 | 15 |
=PEARSON(A1:C1,A2:C2) = 0.968619605
2.
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 17 | 0 | 19 | 25 |
| 2 | 10 | 11 | 7 | 13 |
=PEARSON(A1:D1,A2:D2) = -0.759206026
3.
| A | B | C | |
|---|---|---|---|
| 1 | 1 | 2 | 3 |
| 2 | 4 | 5 |
=PEARSON(A1:C1,A2:B2) = NAN
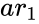 is the array of independent values
is the array of independent values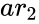 is the array of dependent values.
is the array of dependent values.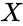 and
and 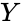 , giving a value between +1 and −1 inclusive.
, giving a value between +1 and −1 inclusive.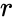 is defined by:
is defined by:
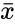 and
and 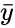 are Average of the two Samples
are Average of the two Samples  and
and 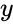 .
.
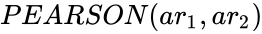 , the value of
, the value of