Difference between revisions of "Manuals/calci/STDEVPA"
Jump to navigation
Jump to search
| Line 33: | Line 33: | ||
|- | |- | ||
! 1 | ! 1 | ||
| − | | 87 || 121 || 427 ||390 || 110|| || | + | | 87 || 121 || 427 ||390 || 110|| 542 || 412 |
|- | |- | ||
! 2 | ! 2 | ||
| 2 || 2.4 || 3.7 ||14.9 || 28 || 198 || 154.1 | | 2 || 2.4 || 3.7 ||14.9 || 28 || 198 || 154.1 | ||
|- | |- | ||
| − | | 5 || 9 || 17 || true || 6 || 0 || 41 | + | | 5 || 9 || 17 || true || 6 || 0 || 41 || 14 |
|} | |} | ||
| Line 46: | Line 46: | ||
#STDEVPA(A3:D3)=5.916079783 | #STDEVPA(A3:D3)=5.916079783 | ||
#STDEVPA(2,12,22,32,false)=11.180339887498949 | #STDEVPA(2,12,22,32,false)=11.180339887498949 | ||
| − | |||
==See Also== | ==See Also== | ||
Revision as of 04:00, 25 January 2014
STDEVPA(n1,n2,n3…)
- are numbers.
Description
- This function gives the standard deviation based on a entire population as the the given data including the logical value and text .
- Standard deviation is a quantity expressing by how much the members of a group differ from the mean value for the group.
- It is the used as a measure of the dispersion or variation in a distribution.
- It is calculated as the square root of variance.
- In , are numbers to find the standard deviation.
- Here is required. are optional.
- Instead of numbers we can use the single array or a reference of a array.
- STDEVPA is defined by the formula: where is the sample mean of and is the total numbers in the given data.
- It is calculated using Failed to parse (syntax error): {\displaystyle "n" } method.
- This function is considering our given data is the entire population.
- Suppose it should consider the data as the sample of the population, we can use the STDEVA function.
- For huge sample sizes the functions and are approximately equal values.
- The arguments can be either numbers or names, array,constants or references that contain numbers.
- Also we can give the text representations of numbers or logical values , like TRUE or FALSE, in a rference.
- Suppose the arguments containing TRUE which is eveluate as 1, and the arguments containing FALSE which is evaluate as 0.
- Suppose the array contains the empty cells and text values like that values are not considered.
- Suppose the function don't want to consider the logical values and text representations of numbers in a reference , we can use the * STDEVP function.
- This function will return the result as error when
1. Any one of the argument is nonnumeric. 2. The arguments containing the error values or text that cannot be translated in to numbers.
Examples
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| 1 | 87 | 121 | 427 | 390 | 110 | 542 | 412 |
| 2 | 2 | 2.4 | 3.7 | 14.9 | 28 | 198 | 154.1 |
| 5 | 9 | 17 | true | 6 | 0 | 41 | 14 |
- STDEVPA(A1:E1)=149.0597195757
- STDEVPA(A2:G2)=76.31463871127
- STDEVPA(A3:D3)=5.916079783
- STDEVPA(2,12,22,32,false)=11.180339887498949
See Also
References
STDEVPA(V1,V2,...)
Where V1,V2......are integers.
This function calculates standard deviation based on the entire population by the given arguments, text and logical values.
- S D is calculated by the "n-1" method.
- The Arguments can be numbers or names, arrays, or references.
- Empty cells, logical values, text, or error values are ignored.
- The text representations of numbers are also counted.
- In this function, TRUE evaluate as 1; and FALSE evaluate as 0 (zero).
- o find STDEVPA, the formula is:
Where x is the sample mean average (V1,V2........) and n is the sample size.
STDEVPA
Lets see an example,
150
130
165
132
110
137
121
?UNIQ7e892969b93851bf-nowiki-00000002-QINU?
Syntax
Remarks
Examples
Description
| Column1 | Column2 | Column3 | Column4 | |
| Row1 | 150 | 16.835337 | ||
| Row2 | 130 | |||
| Row3 | 165 | |||
| Row4 | 132 | |||
| Row5 | 110 | |||
| Row6 | 137 | |||
| Row7 | 121 |
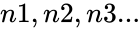 are numbers.
are numbers.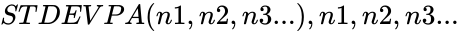 , are numbers to find the standard deviation.
, are numbers to find the standard deviation. is required.
is required. 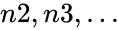 are optional.
are optional.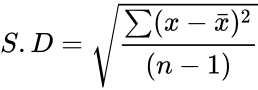 where
where 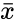 is the sample mean of
is the sample mean of  and
and  is the total numbers in the given data.
is the total numbers in the given data. and
and 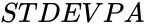 are approximately equal values.
are approximately equal values.