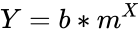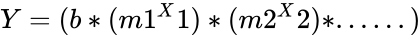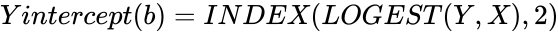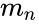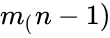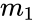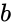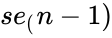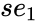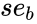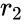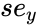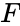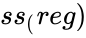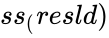Difference between revisions of "Manuals/calci/LOGEST"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''LOGEST'''('''Y, X''',C,stats) '''Where Y''' is the set of y-values and X is an optional set of x-values in...") |
|||
| Line 1: | Line 1: | ||
| − | + | =LOGEST(Y, X, C , stats)= | |
| − | + | where, | |
| + | *<math>Y</math> is a set of Y values, | ||
| + | *<math>X</math> is an optional set of X values, | ||
| + | *<math>C</math> is a logical value TRUE or FALSE, that decides whether to force the constant 'b' to 1, | ||
| + | *<math>stats</math> is a logical value TRUE or FALSE, that decides whether to return additional regression statistics. | ||
| − | + | LOGEST() is an array function that calculates the exponential curve that fits the data values and returns an array of values that describes the curve. | |
| − | + | == Description == | |
| − | |||
| − | |||
| − | + | *If 'Y' is dependent variable, 'X' is independent variable, 'm' is a constant base for X value and 'b' is constant (Y-intercept), | |
| + | then equation for curve is - | ||
| − | + | <math>Y= b*m^X</math> | |
| − | |||
| − | < | ||
| − | + | *For multiple ranges of X-values, | |
| − | Y | + | <math>Y = (b*(m1^X1)*(m2^X2)*......)</math> |
| + | *Argument values <math>X</math> and <math>Y</math> should be numeric, else Calci displays an error message. | ||
| + | *The length of array of X values should be equal to length of array of Y values, else Calci displays an error message. | ||
| + | *<math>C</math> is a logical value that decides whether to make constant 'b' equal to 1. | ||
| + | *If <math>C</math> = TRUE or omitted, 'b' is calculated normally. If <math>C</math> = FALSE, 'b' is made equal to 1. | ||
| + | *<math>stats</math> is a logical value that decides whether to display additional regression statistics. | ||
| + | *If <math>stats</math> = TRUE, calci returns additional regresstion statistics. If <math>stats</math> = FALSE or omitted, Calci returns the values of 'm coefficients' and the constant 'b'. | ||
| + | *When there is only one independent X variable, Slope(m) and Y intercept (b) can be calculated using following formulas - | ||
| − | + | <math>Y intercept (b) = INDEX(LOGEST(Y, X),2) </math> | |
| + | *The additional regression | ||
| − | </ | + | {| class="wikitable" |
| − | ---- | + | |- |
| − | < | + | | <math>m_n</math> || <math>m_(n-1)</math> || --- || <math>m_1</math> || <math>b</math> |
| + | |- | ||
| + | | <math>se_n</math> || <math>se_(n-1)</math> || --- || <math>se_1</math> || <math>se_b</math> | ||
| + | |- | ||
| + | | <math>r_2</math> || <math>se_y</math> || || || | ||
| + | |- | ||
| + | | <math>F</math> || <math>d_f</math> || || || | ||
| + | |- | ||
| + | | <math>ss_(reg)</math> || <math>ss_(resld)</math> || || || | ||
| + | |} | ||
| − | + | where each statistic value is described below- | |
| + | <math>m_n</math> is an array of constant base values for curve equation | ||
| + | <math>b</math> is the constant value of Y when X=0 | ||
| + | <math>se_1</math> is the standard error value for m1 | ||
| + | <math>se_b</math> is the standard error value for constant b | ||
| + | <math>r_2</math> is the coefficient of determination | ||
| + | <math>se_y</math> is the standard error value for Y estimate | ||
| + | <math>F</math> is the observed F value | ||
| + | <math>d_f</math> is the number of degrees of freedom | ||
| + | <math>ss_(reg)</math> is the regression sum of squares | ||
| + | <math>ss_(resld)</math> is the residual sum of squares | ||
| − | + | == Examples == | |
| − | |||
| − | |||
| − | < | + | <div id="2SpaceContent" class="zcontent" align="left"> |
| − | + | {| id="TABLE3" class="SpreadSheet blue" | |
| + | |- class="even" | ||
| + | | class="sshl_f" | '''X1 values''' | ||
| + | | class="sshl_f" | '''X2 values''' | ||
| + | | class="sshl_f" | '''Y values''' | ||
| + | | class="sshl_f" | | ||
| − | + | |- class="odd" | |
| + | | class="sshl_f" | 1 | ||
| + | | class="sshl_f" | 15 | ||
| + | | class="sshl_f" | 5 | ||
| + | | class="sshl_f" | | ||
| − | + | |- class="even" | |
| + | | class="sshl_f" | 2 | ||
| + | | class="sshl_f" | 17 | ||
| + | | class="sshl_f" | 9 | ||
| + | | class="sshl_f" | | ||
| − | + | |- class="odd" | |
| + | | class="sshl_f" | 3 | ||
| + | | class="sshl_f" | 23 | ||
| + | | class="sshl_f" | 11 | ||
| + | | class="sshl_f" | | ||
| − | + | |- class="even" | |
| + | | class="sshl_f" | 4 | ||
| + | | class="sshl_f" | 28 | ||
| + | | class="sshl_f" | 16 | ||
| + | | class="sshl_f" | | ||
| − | + | |- class="odd" | |
| + | | class="sshl_f" | 5 | ||
| + | | class="sshl_f" | 30 | ||
| + | | class="sshl_f" | 20 | ||
| + | | class="sshl_f" | | ||
| + | |} | ||
| − | + | Example with single range of X values: | |
| − | + | =LOGEST(C2:C6,A2:A6,TRUE,TRUE) : Displays all the regression statistics for curve with Y values in cell range C2 to C6 and X values in the cell range A2 to A6. | |
| − | < | + | <div id="5SpaceContent" class="zcontent" align="left"> |
| − | + | {| class="SpreadSheet blue" | |
| − | + | |- class="even" | |
| − | + | | 1.3976542375431584 | |
| − | - | + | | 4.015612511401349 |
| − | + | |- class="odd" | |
| − | + | | 0.035964826100314505 | |
| − | + | | 0.11928183382512401 | |
| − | - | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- class="even" | |- class="even" | ||
| − | | | + | | 0.9665390759484563 |
| − | + | | 0.11373076612886521 | |
| − | |||
| − | | | ||
| − | |||
|- class="odd" | |- class="odd" | ||
| − | | class=" " | | + | | 86.65681866342828 |
| − | | | + | | 3 |
| − | + | |- class="even" | |
| − | + | | 1.1208788400613339 | |
| − | | class=" | + | | 0.038804061492775904 |
| + | |||
| + | |} | ||
| + | |||
| + | Example with multiple range of X values: | ||
| + | |||
| + | =LOGEST(C2:C6,A2:B6,TRUE,TRUE) : Displays all the regression statistics for curve with Y values in cell range C2 to C6 and X values in the cell range A2 to B6. | ||
| + | <div id="5SpaceContent" class="zcontent" align="left"> | ||
| + | |||
| + | {| class="SpreadSheet blue" | ||
|- class="even" | |- class="even" | ||
| − | | | + | | 0.9684996526566505 |
| − | + | | 1.593646236498643 | |
| − | | | ||
| − | |||
| − | |||
|- class="odd" | |- class="odd" | ||
| − | | | + | | 0.05737674420683413 |
| − | | | + | | 0.23878654115432985 |
| − | |||
| − | |||
| − | |||
|- class="even" | |- class="even" | ||
| − | | | + | | 0.9710443899207976 |
| − | | | + | | 0.12957493182116453 |
| − | |||
| − | |||
| − | |||
|- class="odd" | |- class="odd" | ||
| − | | | + | | 33.53562184546261 |
| − | + | | 2 | |
| − | | | ||
| − | |||
| − | |||
|- class="even" | |- class="even" | ||
| − | | | + | | 1.1261035756411908 |
| − | | | + | | 0.03357932591291887 |
| − | |||
| − | |||
| − | |||
|} | |} | ||
| + | |||
| + | == See Also == | ||
| + | |||
| + | *[[Manuals/calci/LOGEST| LOGEST]] | ||
| − | + | == References == | |
| − | + | *[http://en.wikipedia.org/wiki/Curve Curve] | |
| + | *[http://en.wikipedia.org/wiki/Curve_fitting Curve Fitting] | ||
| + | *[http://en.wikipedia.org/wiki/Linear_equation Linear Equation] | ||
Revision as of 18:14, 29 January 2014
LOGEST(Y, X, C , stats)
where,
- is a set of Y values,
- is an optional set of X values,
- is a logical value TRUE or FALSE, that decides whether to force the constant 'b' to 1,
- is a logical value TRUE or FALSE, that decides whether to return additional regression statistics.
LOGEST() is an array function that calculates the exponential curve that fits the data values and returns an array of values that describes the curve.
Description
- If 'Y' is dependent variable, 'X' is independent variable, 'm' is a constant base for X value and 'b' is constant (Y-intercept),
then equation for curve is -
- For multiple ranges of X-values,
- Argument values and should be numeric, else Calci displays an error message.
- The length of array of X values should be equal to length of array of Y values, else Calci displays an error message.
- is a logical value that decides whether to make constant 'b' equal to 1.
- If = TRUE or omitted, 'b' is calculated normally. If = FALSE, 'b' is made equal to 1.
- is a logical value that decides whether to display additional regression statistics.
- If = TRUE, calci returns additional regresstion statistics. If = FALSE or omitted, Calci returns the values of 'm coefficients' and the constant 'b'.
- When there is only one independent X variable, Slope(m) and Y intercept (b) can be calculated using following formulas -
- The additional regression
| --- | ||||
| --- | ||||
where each statistic value is described below- is an array of constant base values for curve equation is the constant value of Y when X=0 is the standard error value for m1 is the standard error value for constant b is the coefficient of determination is the standard error value for Y estimate is the observed F value is the number of degrees of freedom is the regression sum of squares is the residual sum of squares
Examples
| X1 values | X2 values | Y values | |
| 1 | 15 | 5 | |
| 2 | 17 | 9 | |
| 3 | 23 | 11 | |
| 4 | 28 | 16 | |
| 5 | 30 | 20 |
Example with single range of X values:
=LOGEST(C2:C6,A2:A6,TRUE,TRUE) : Displays all the regression statistics for curve with Y values in cell range C2 to C6 and X values in the cell range A2 to A6.
| 1.3976542375431584 | 4.015612511401349 |
| 0.035964826100314505 | 0.11928183382512401 |
| 0.9665390759484563 | 0.11373076612886521 |
| 86.65681866342828 | 3 |
| 1.1208788400613339 | 0.038804061492775904 |
Example with multiple range of X values:
=LOGEST(C2:C6,A2:B6,TRUE,TRUE) : Displays all the regression statistics for curve with Y values in cell range C2 to C6 and X values in the cell range A2 to B6.
| 0.9684996526566505 | 1.593646236498643 |
| 0.05737674420683413 | 0.23878654115432985 |
| 0.9710443899207976 | 0.12957493182116453 |
| 33.53562184546261 | 2 |
| 1.1261035756411908 | 0.03357932591291887 |
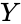 is a set of Y values,
is a set of Y values,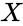 is an optional set of X values,
is an optional set of X values, is a logical value TRUE or FALSE, that decides whether to force the constant 'b' to 1,
is a logical value TRUE or FALSE, that decides whether to force the constant 'b' to 1,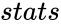 is a logical value TRUE or FALSE, that decides whether to return additional regression statistics.
is a logical value TRUE or FALSE, that decides whether to return additional regression statistics.