Difference between revisions of "Manuals/calci/STDEVPA"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''STDEVPA(n1,n2,n3…)'''</div><br/> | <div style="font-size:30px">'''STDEVPA(n1,n2,n3…)'''</div><br/> | ||
*<math>n1,n2,n3... </math> are numbers. | *<math>n1,n2,n3... </math> are numbers. | ||
| − | |||
==Description== | ==Description== | ||
| − | *This function gives the standard deviation based on a entire population | + | *This function gives the standard deviation based on a entire population as the given data including the logical value and text . |
| − | *Standard | + | *Standard Deviation is a quantity expressing by how much the members of a group differ from the mean value for the group. |
*It is the used as a measure of the dispersion or variation in a distribution. | *It is the used as a measure of the dispersion or variation in a distribution. | ||
*It is calculated as the square root of variance. | *It is calculated as the square root of variance. | ||
| − | *In <math> STDEVPA(n1,n2,n3...), n1,n2,n3...</math>, are numbers to find the standard deviation. | + | *In <math> STDEVPA(n1,n2,n3...)</math>, <math>n1,n2,n3...</math>, are numbers to find the standard deviation. |
*Here <math> n1</math> is required. <math> n2,n3,...</math> are optional. | *Here <math> n1</math> is required. <math> n2,n3,...</math> are optional. | ||
*Instead of numbers we can use the single array or a reference of a array. | *Instead of numbers we can use the single array or a reference of a array. | ||
| − | *STDEVPA is defined by the formula: <math>S.D= \sqrt \frac {\sum(x-\bar{x})^2}{(n-1)} </math> where <math> \bar{x} </math> is the sample mean of <math> x </math> and <math> n </math> is the total | + | *STDEVPA is defined by the formula: |
| + | <math>S.D= \sqrt \frac {\sum(x-\bar{x})^2}{(n-1)} </math> | ||
| + | where <math> \bar{x} </math> is the sample mean of <math> x </math> and <math> n </math> is the total number in the given data. | ||
*It is calculated using <math> "n" </math> method. | *It is calculated using <math> "n" </math> method. | ||
*This function is considering our given data is the entire population. | *This function is considering our given data is the entire population. | ||
| Line 17: | Line 18: | ||
*For huge sample sizes the functions <math> STDEVA </math> and <math> STDEVPA </math> are approximately equal values. | *For huge sample sizes the functions <math> STDEVA </math> and <math> STDEVPA </math> are approximately equal values. | ||
*The arguments can be either numbers or names, array,constants or references that contain numbers. | *The arguments can be either numbers or names, array,constants or references that contain numbers. | ||
| − | *Also we can give the text representations of numbers or logical values , like TRUE or FALSE, in a | + | *Also we can give the text representations of numbers or logical values , like TRUE or FALSE, in a reference. |
| − | *Suppose the arguments containing TRUE which is | + | *Suppose the arguments containing TRUE which is evaluate as 1, and the arguments containing FALSE which is evaluate as 0. |
*Suppose the array contains the empty cells and text values like that values are not considered. | *Suppose the array contains the empty cells and text values like that values are not considered. | ||
*Suppose the function don't want to consider the logical values and text representations of numbers in a reference , we can use the *[[Manuals/calci/STDEVP | STDEVP ]] function. | *Suppose the function don't want to consider the logical values and text representations of numbers in a reference , we can use the *[[Manuals/calci/STDEVP | STDEVP ]] function. | ||
*This function will return the result as error when | *This function will return the result as error when | ||
| − | 1. Any one of the argument is | + | 1. Any one of the argument is non-numeric. |
2. The arguments containing the error values or text that cannot be translated in to numbers. | 2. The arguments containing the error values or text that cannot be translated in to numbers. | ||
| Line 42: | Line 43: | ||
| − | #STDEVPA(A1:E1)=149.0597195757 | + | #=STDEVPA(A1:E1) = 149.0597195757 |
| − | #STDEVPA(A2:G2)=76.31463871127 | + | #=STDEVPA(A2:G2) = 76.31463871127 |
| − | #STDEVPA(A3:D3)=5.916079783 | + | #=STDEVPA(A3:D3) = 5.916079783 |
| − | #STDEVPA(2,12,22,32,false)=11.180339887498949 | + | #=STDEVPA(2,12,22,32,false) = 11.180339887498949 |
==See Also== | ==See Also== | ||
| Line 52: | Line 53: | ||
*[[Manuals/calci/STDEVP | STDEVP ]] | *[[Manuals/calci/STDEVP | STDEVP ]] | ||
*[[Manuals/calci/STDEVA| STDEVA]] | *[[Manuals/calci/STDEVA| STDEVA]] | ||
| − | |||
| − | |||
==References== | ==References== | ||
Revision as of 04:47, 30 January 2014
STDEVPA(n1,n2,n3…)
- are numbers.
Description
- This function gives the standard deviation based on a entire population as the given data including the logical value and text .
- Standard Deviation is a quantity expressing by how much the members of a group differ from the mean value for the group.
- It is the used as a measure of the dispersion or variation in a distribution.
- It is calculated as the square root of variance.
- In , , are numbers to find the standard deviation.
- Here is required. are optional.
- Instead of numbers we can use the single array or a reference of a array.
- STDEVPA is defined by the formula:
where is the sample mean of and is the total number in the given data.
- It is calculated using Failed to parse (syntax error): {\displaystyle "n" } method.
- This function is considering our given data is the entire population.
- Suppose it should consider the data as the sample of the population, we can use the STDEVA function.
- For huge sample sizes the functions and are approximately equal values.
- The arguments can be either numbers or names, array,constants or references that contain numbers.
- Also we can give the text representations of numbers or logical values , like TRUE or FALSE, in a reference.
- Suppose the arguments containing TRUE which is evaluate as 1, and the arguments containing FALSE which is evaluate as 0.
- Suppose the array contains the empty cells and text values like that values are not considered.
- Suppose the function don't want to consider the logical values and text representations of numbers in a reference , we can use the * STDEVP function.
- This function will return the result as error when
1. Any one of the argument is non-numeric. 2. The arguments containing the error values or text that cannot be translated in to numbers.
Examples
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| 1 | 87 | 121 | 427 | 390 | 110 | 542 | 412 |
| 2 | 2 | 2.4 | 3.7 | 14.9 | 28 | 198 | 154.1 |
| 5 | 9 | 17 | true | 6 | 0 | 41 | 14 |
- =STDEVPA(A1:E1) = 149.0597195757
- =STDEVPA(A2:G2) = 76.31463871127
- =STDEVPA(A3:D3) = 5.916079783
- =STDEVPA(2,12,22,32,false) = 11.180339887498949
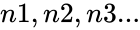 are numbers.
are numbers.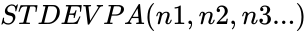 ,
,  is required.
is required. 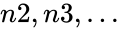 are optional.
are optional.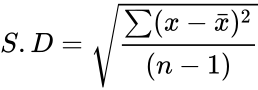 where
where 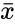 is the sample mean of
is the sample mean of  and
and  is the total number in the given data.
is the total number in the given data.
 and
and  are approximately equal values.
are approximately equal values.