Difference between revisions of "Manuals/calci/TDIST"
Jump to navigation
Jump to search
| Line 3: | Line 3: | ||
*<math> df </math> is the degrees of freedom. | *<math> df </math> is the degrees of freedom. | ||
*<math> t </math> is the number of tails. | *<math> t </math> is the number of tails. | ||
| − | |||
==Description== | ==Description== | ||
| − | *This function gives the value of the | + | *This function gives the value of the T-Distribution. |
*It is the continuous probability distributions. | *It is the continuous probability distributions. | ||
| − | *The | + | *The T-Distribution is also called Students T-Distribution. |
| − | *This is the symmetric distribution like the | + | *This is the symmetric distribution like the Normal Distribution. |
*It is used when making inferences about a population mean when the population standard deviation is not known. | *It is used when making inferences about a population mean when the population standard deviation is not known. | ||
| − | *In <math> TDIST(x,df,t), x </math> is the numeric value to find the value of the distribution. | + | *In <math> TDIST(x,df,t)</math>, <math>x </math> is the numeric value to find the value of the distribution. |
*<math> df </math> is the integer which is indicating the number of degrees of freedom and <math> t </math> is indicating the number of distribution tails. | *<math> df </math> is the integer which is indicating the number of degrees of freedom and <math> t </math> is indicating the number of distribution tails. | ||
| − | *Suppose t=1, then this distribution is | + | *Suppose t=1, then this distribution is One-Tailed Distribution and t=2, then this is Two-Tailed Distribution. |
| − | *Also t=1, then it is calculated as <math> TDIST=P(X>x) </math>, where <math> X </math> is a random variable that follows the | + | *Also t=1, then it is calculated as <math> TDIST=P(X>x) </math>, where <math> X </math> is a random variable that follows the T-Distribution. |
*And t=2, then it is calculated as <math> TDIST =P(X>x or X<-x) </math>. | *And t=2, then it is calculated as <math> TDIST =P(X>x or X<-x) </math>. | ||
*This function will return the result as error | *This function will return the result as error | ||
| − | 1. Any one of the argument is | + | 1. Any one of the argument is non-numeric. |
| − | 2. df<1 and x<0. When we are giving df and t as a decimals, then it is changing in to integers. | + | 2. df<1 and x<0. When we are giving <math>df</math> and <math>t</math> as a decimals, then it is changing in to integers. |
==Examples== | ==Examples== | ||
| − | #TDIST(1.82,55,1) = 0.037101192599 | + | #=TDIST(1.82,55,1) = 0.037101192599 |
| − | #TDIST(1.82,55,2) = 0.074202385199 | + | #=TDIST(1.82,55,2) = 0.074202385199 |
| − | #TDIST(5.9812,75,1)= 3.50350792266e-8 | + | #=TDIST(5.9812,75,1)= 3.50350792266e-8 |
| − | #TDIST(5.9812,75,2) = 7.007015845328e-8 | + | #=TDIST(5.9812,75,2) = 7.007015845328e-8 |
| − | #TDIST(2.4579,20.4,1) = 0.0122238 | + | #=TDIST(2.4579,20.4,1) = 0.0122238 |
| − | #TDIST(2.4579,20.4,1.2) = Null | + | #=TDIST(2.4579,20.4,1.2) = Null |
| − | |||
| − | |||
==See Also== | ==See Also== | ||
*[[Manuals/calci/TTEST | TTEST]] | *[[Manuals/calci/TTEST | TTEST]] | ||
*[[Manuals/calci/TINV | TINV ]] | *[[Manuals/calci/TINV | TINV ]] | ||
| − | |||
| − | |||
==References== | ==References== | ||
Revision as of 06:04, 30 January 2014
TDIST(x,df,t),
- is the numeric value to find the distribution.
- is the degrees of freedom.
- is the number of tails.
Description
- This function gives the value of the T-Distribution.
- It is the continuous probability distributions.
- The T-Distribution is also called Students T-Distribution.
- This is the symmetric distribution like the Normal Distribution.
- It is used when making inferences about a population mean when the population standard deviation is not known.
- In , is the numeric value to find the value of the distribution.
- is the integer which is indicating the number of degrees of freedom and is indicating the number of distribution tails.
- Suppose t=1, then this distribution is One-Tailed Distribution and t=2, then this is Two-Tailed Distribution.
- Also t=1, then it is calculated as , where is a random variable that follows the T-Distribution.
- And t=2, then it is calculated as .
- This function will return the result as error
1. Any one of the argument is non-numeric.
2. df<1 and x<0. When we are giving and as a decimals, then it is changing in to integers.
Examples
- =TDIST(1.82,55,1) = 0.037101192599
- =TDIST(1.82,55,2) = 0.074202385199
- =TDIST(5.9812,75,1)= 3.50350792266e-8
- =TDIST(5.9812,75,2) = 7.007015845328e-8
- =TDIST(2.4579,20.4,1) = 0.0122238
- =TDIST(2.4579,20.4,1.2) = Null
 is the numeric value to find the distribution.
is the numeric value to find the distribution.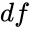 is the degrees of freedom.
is the degrees of freedom.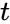 is the number of tails.
is the number of tails.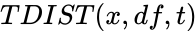 ,
, 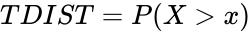 , where
, where 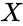 is a random variable that follows the T-Distribution.
is a random variable that follows the T-Distribution.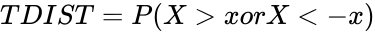 .
.