Difference between revisions of "Manuals/calci/SQRTPI"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''SQRTPI(n)'''</div><br/> | <div style="font-size:30px">'''SQRTPI(n)'''</div><br/> | ||
| − | *<math>n </math> | + | *<math>n </math> is the number. |
| Line 14: | Line 14: | ||
==Examples== | ==Examples== | ||
| − | #SQRTPI(1)=1.772453851 | + | #=SQRTPI(1) = 1.772453851 |
| − | #SQRTPI(0)=0 | + | #=SQRTPI(0) = 0 |
| − | #SQRTPI(5)= 3.963327298 | + | #=SQRTPI(5) = 3.963327298 |
| − | #SQRTPI(-2)=NAN | + | #=SQRTPI(-2) = NAN |
Revision as of 03:37, 3 February 2014
SQRTPI(n)
- is the number.
Description
- This function gives the square root of .
- The is a mathematical constant with a value approximate to 3.14159.
- In is the number by which is multipled.When we are omitting the value of ,then it will consider the value n=1.
- is denoted by the Greek letter Failed to parse (syntax error): {\displaystyle π} .
- Failed to parse (syntax error): {\displaystyle π } is a transcendental number and irrational number.
- Being an irrational number,Failed to parse (syntax error): {\displaystyle π } cannot be expressed exactly as a ratio of any two integers ,but we can express as the fraction 22/7 is approximate to the π value , also no fraction can be its exact value.
This function will give the result as error when n<0.
Examples
- =SQRTPI(1) = 1.772453851
- =SQRTPI(0) = 0
- =SQRTPI(5) = 3.963327298
- =SQRTPI(-2) = NAN
See Also
 is the number.
is the number.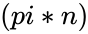 .
.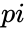 is a mathematical constant with a value approximate to 3.14159.
is a mathematical constant with a value approximate to 3.14159.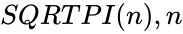 is the number by which
is the number by which 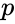 is multipled.When we are omitting the value of
is multipled.When we are omitting the value of 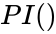 is denoted by the Greek letter Failed to parse (syntax error): {\displaystyle π}
.
is denoted by the Greek letter Failed to parse (syntax error): {\displaystyle π}
.