Difference between revisions of "Manuals/calci/VAR"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*Variance is a measure of dispersion obtained by taking the mean of the squared deviations of the observed values from their mean in a frequency distribution. | *Variance is a measure of dispersion obtained by taking the mean of the squared deviations of the observed values from their mean in a frequency distribution. | ||
*i.e.,variance is a measure of how far each value in the data set is from the mean. | *i.e.,variance is a measure of how far each value in the data set is from the mean. | ||
| − | *It is denoted by | + | *It is denoted by <math> \sigma </math>. The square root of variance is called the standard deviation. |
| − | *In VAR(n1,n2,n3,...) ,n1,n2,n3,... are numbers based on a sample of a population. Here n1 is required.n2,n3,... are optional. | + | *In <math>VAR(n1,n2,n3,...)</math>, <math>n1,n2,n3,...</math> are numbers based on a sample of a population. Here <math>n1</math> is required. <math>n2,n3,...</math> are optional. |
*To find the variance we can use the following formula: | *To find the variance we can use the following formula: | ||
| − | Variance= | + | <math>Variance= \frac{\sum (x_i-\bar{x})^2}{n-1}</math> |
| − | where x | + | where <math> \bar{x}</math> is the sample mean of <math>x)i<\math> and <math> n </math> is the sample size. |
| − | *Suppose | + | *Suppose <math>\sigma = 0<\math> which is indicating all the values are identical. |
| − | *When | + | *When <math>\sigma </math> is non-zero then it is always positive. |
*This function is considering our given data is the sample of the population. | *This function is considering our given data is the sample of the population. | ||
| − | *Suppose it should consider the data as the entire population, we can use the VARP function. | + | *Suppose it should consider the data as the entire population, we can use the [[Manuals/calci/VARP | VARP ]] function. |
*The arguments can be be either numbers or names, array,constants or references that contain numbers. | *The arguments can be be either numbers or names, array,constants or references that contain numbers. | ||
*Suppose the array contains text,logical values or empty cells, like that values are not considered. | *Suppose the array contains text,logical values or empty cells, like that values are not considered. | ||
*When we are entering logical values and text representations of numbers as directly, then the arguments are counted. | *When we are entering logical values and text representations of numbers as directly, then the arguments are counted. | ||
| − | *Suppose the function have to consider the logical values and text representations of numbers in a reference , we can use the VARA function. | + | *Suppose the function have to consider the logical values and text representations of numbers in a reference , we can use the [[Manuals/calci/VARA | VARA ]] function. |
*This function will return the result as error when | *This function will return the result as error when | ||
1. Any one of the argument is nonnumeric. | 1. Any one of the argument is nonnumeric. | ||
| Line 25: | Line 25: | ||
==Examples== | ==Examples== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
|+Spreadsheet | |+Spreadsheet | ||
| Line 50: | Line 39: | ||
| 50 || 58 || 81 || true || 12 || 81 || 10 || 27 || 24 || 39 | | 50 || 58 || 81 || true || 12 || 81 || 10 || 27 || 24 || 39 | ||
|} | |} | ||
| + | #VAR(A1:J1)=756.6222222223 | ||
| + | #VAR(A2:E2)=21.0852299999 | ||
| + | #VAR(A3:C4)= 259 | ||
| + | #VAR(A3:C3)=259 | ||
| + | #VAR(10,25,18,FALSE) =141.592592 | ||
| + | #VAR(10,25,18,TRUE)=107 | ||
Revision as of 00:07, 7 February 2014
VAR(n1,n2,n3…)
- are numbers.
Description
- This function gives the variance based on a sample.
- Variance is a measure of dispersion obtained by taking the mean of the squared deviations of the observed values from their mean in a frequency distribution.
- i.e.,variance is a measure of how far each value in the data set is from the mean.
- It is denoted by . The square root of variance is called the standard deviation.
- In , are numbers based on a sample of a population. Here is required. are optional.
- To find the variance we can use the following formula:
where is the sample mean of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x)i<\math> and <math> n } is the sample size.
- Suppose Failed to parse (unknown function "\math"): {\displaystyle \sigma = 0<\math> which is indicating all the values are identical. *When <math>\sigma } is non-zero then it is always positive.
- This function is considering our given data is the sample of the population.
- Suppose it should consider the data as the entire population, we can use the VARP function.
- The arguments can be be either numbers or names, array,constants or references that contain numbers.
- Suppose the array contains text,logical values or empty cells, like that values are not considered.
- When we are entering logical values and text representations of numbers as directly, then the arguments are counted.
- Suppose the function have to consider the logical values and text representations of numbers in a reference , we can use the VARA function.
- This function will return the result as error when
1. Any one of the argument is nonnumeric.
2. The arguments containing the error values or text that cannot be translated in to numbers.
Examples
| A | B | C | D | E | F | G | H | I | J | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 78 | 61 | 53 | 46 | 24 | 19 | 82 | 90 | 45 | 10 |
| 2 | 10.25 | 16.74 | 18.09 | 20.43 | 22.22 | 11.98 | 24 | 19 | 10 | 75 |
| 3 | 50 | 58 | 81 | true | 12 | 81 | 10 | 27 | 24 | 39 |
- VAR(A1:J1)=756.6222222223
- VAR(A2:E2)=21.0852299999
- VAR(A3:C4)= 259
- VAR(A3:C3)=259
- VAR(10,25,18,FALSE) =141.592592
- VAR(10,25,18,TRUE)=107
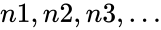 are numbers.
are numbers.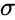 . The square root of variance is called the standard deviation.
. The square root of variance is called the standard deviation.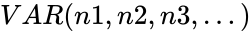 ,
,  is required.
is required. 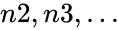 are optional.
are optional.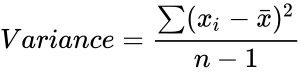 where
where 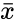 is the sample mean of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x)i<\math> and <math> n }
is the sample size.
is the sample mean of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x)i<\math> and <math> n }
is the sample size.