Difference between revisions of "Manuals/calci/ZTESTEQUALMEANS"
| Line 13: | Line 13: | ||
3.Both populations are normally distributed or both sample sizes are large enough that the means are normally distributed. | 3.Both populations are normally distributed or both sample sizes are large enough that the means are normally distributed. | ||
*In <math> ZTESTTWOSAMPLEFORMEANS(ar_1,ar_2,v_1,v_2,md,alpha,lv)</math>,<math> ar_1 </math> and <math>ar_2</math> are the set of values,<math>v_1</math> is the variance of <math>ar_1</math>,<math>v_2</math> is the variance of <math>ar_2</math>. | *In <math> ZTESTTWOSAMPLEFORMEANS(ar_1,ar_2,v_1,v_2,md,alpha,lv)</math>,<math> ar_1 </math> and <math>ar_2</math> are the set of values,<math>v_1</math> is the variance of <math>ar_1</math>,<math>v_2</math> is the variance of <math>ar_2</math>. | ||
| − | *<math> md <math> is the Hypothesized Mean Difference. If testing is for equal means,then <math>md = 0</math>. | + | *<math> md </math> is the Hypothesized Mean Difference. If testing is for equal means,then <math>md = 0</math>. |
*<math>alpha</math> is the significance level which ranges from 0 to 1. | *<math>alpha</math> is the significance level which ranges from 0 to 1. | ||
*<math>lv</math> is the logical value like TRUE or FALSE.TRUE is indicating the result will display in new worksheet. | *<math>lv</math> is the logical value like TRUE or FALSE.TRUE is indicating the result will display in new worksheet. | ||
*Suppose we are omitted the <math>lv</math> value it will consider the value as FALSE. | *Suppose we are omitted the <math>lv</math> value it will consider the value as FALSE. | ||
*ZTEST two sample for means is calculated by:<math> z=\frac{\bar{x_1}-\bar{x_2}-\Delta}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}</math> | *ZTEST two sample for means is calculated by:<math> z=\frac{\bar{x_1}-\bar{x_2}-\Delta}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}</math> | ||
| − | where <math>\bar{x_1}</math> and <math>\bar{x_2}<\math> are average of two samples,<math>\Delta</math> is the Hypothesized Mean Difference between two means of the population. <math>\sigma_1</math> and <math>\sigma_2</math> are the standard deviation of two population. <math>n_1<\math> and <math>n_2<\math> are the sizes of the samples. | + | where <math>\bar{x_1}</math> and <math>\bar{x_2}<\math> are average of two samples, <math>\Delta</math> is the Hypothesized Mean Difference between two means of the population. <math>\sigma_1</math> and <math>\sigma_2</math> are the standard deviation of two population. <math> n_1 <\math> and <math> n_2 <\math> are the sizes of the samples. |
*This function will give the result as error when | *This function will give the result as error when | ||
1. any one of the argument is nonnumeric. | 1. any one of the argument is nonnumeric. | ||
Revision as of 23:42, 9 February 2014
- and are array of values.
- and are value of variances.
- is the Hypothesized Mean Difference.
- is the significance level.
- is the logical value.
Description
- This function gives the z-test two sample for means.
- We can use this test when
1.The samples can be different sizes. 2.The two samples are independent. 3.Both populations are normally distributed or both sample sizes are large enough that the means are normally distributed.
- In , and are the set of values, is the variance of , is the variance of .
- is the Hypothesized Mean Difference. If testing is for equal means,then .
- is the significance level which ranges from 0 to 1.
- is the logical value like TRUE or FALSE.TRUE is indicating the result will display in new worksheet.
- Suppose we are omitted the value it will consider the value as FALSE.
- ZTEST two sample for means is calculated by:
where and Failed to parse (unknown function "\math"): {\displaystyle \bar{x_2}<\math> are average of two samples, <math>\Delta} is the Hypothesized Mean Difference between two means of the population. and are the standard deviation of two population. <math> n_1 <\math> and <math> n_2 <\math> are the sizes of the samples.
- This function will give the result as error when
1. any one of the argument is nonnumeric. 2. alpha>1
and ar2 are array of values, and v2 , , and
ZTESTTWOSAMPLEFORMEANS(Array1, Array2, Variance1, Variance2, Alpha, NewTableFlag)
where,
Array1 - Input range should be one block.
Array2 - Input range should be one block.
Variance1 - Input range should be one block.
Variance2 - Input range should be one block.
HypothesizeDiff - represents the Hypothesized Mean Difference.A value 0 indicates that sample means are hypothesized to be equal.
Alpha - represents the significance level and value in range 0 to 1.
' 'NewTableFlag - is the TRUE or FALSE.If set as TRUE,the result in new sheet. If NewTableFlag is omitted, it assumed to be FALSE.Lets see an example in (Column4Row5)
?UNIQbb01b3076906c32b-nowiki-00000004-QINU?
ZTESTTWOSAMPLESFORMEANS returns the result in new sheet(5Space).
?UNIQbb01b3076906c32b-nowiki-00000005-QINU?
ZTESTTWOSAMPLESFORMEANS returns the #ERROR(Alpha = -0.055).
Z-TEST : TWO SAMPLE FOR MEANS
If the Alpha < 0 or Alpha >1, ZTESTTWOSAMPLEFORMEANS returns the #ERROR.
| Column1 | Column2 | Column3 | Column4 | |
| Row1 | 10 | 3 | 1 | 8 |
| Row2 | 7 | 8 | 2 | 9 |
| Row3 | 12 | 8 | 3 | 10 |
| Row4 | 17 | 18 | 4 | 11 |
| Row5 | 46 | 34 | 5Space | |
| Row6 | 6 | 7 | #ERROR |
| Variable1 | Variable2 | |
|---|---|---|
| Mean | 11.5 | 9.25 |
| Known Variance | 1,2,3,4 | 8,9,10,11 |
| Observations | 4 | 4 |
| Hypothesized Mean Difference | 0 | |
| z Value | NaN | |
| P(T<=t) One-tail | 0 | |
| z Critical One-tail | 1.6448536269514715 | |
| P(T<=t) Two-tail | 0 | |
| z Critical Two-tail | 1.9599639845400536 |
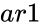 and
and 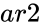 are array of values.
are array of values.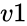 and
and 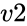 are value of variances.
are value of variances.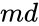 is the Hypothesized Mean Difference.
is the Hypothesized Mean Difference.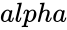 is the significance level.
is the significance level. is the logical value.
is the logical value.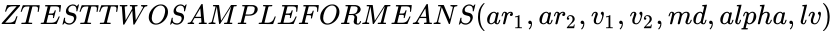 ,
,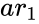 and
and 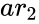 are the set of values,
are the set of values,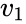 is the variance of
is the variance of 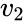 is the variance of
is the variance of 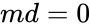 .
.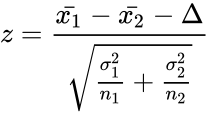
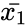 and Failed to parse (unknown function "\math"): {\displaystyle \bar{x_2}<\math> are average of two samples, <math>\Delta}
is the Hypothesized Mean Difference between two means of the population.
and Failed to parse (unknown function "\math"): {\displaystyle \bar{x_2}<\math> are average of two samples, <math>\Delta}
is the Hypothesized Mean Difference between two means of the population. 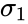 and
and 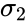 are the standard deviation of two population. <math> n_1 <\math> and <math> n_2 <\math> are the sizes of the samples.
are the standard deviation of two population. <math> n_1 <\math> and <math> n_2 <\math> are the sizes of the samples.