Difference between revisions of "Manuals/calci/FOURIERANALYSIS"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''FOURIERANALYSIS'''(Array, NewTableFlag) where, '''Array '''- Input range should be one or more blocks. ...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''FOURIERANALYSIS(n1,n2,n3,n4,…)'''</div><br/> |
| + | *<math>n1,n2,n3,n4…</math> are real numbers. | ||
| − | + | ==Description== | |
| − | + | *This function gives the value of the discrete fourier tranform. | |
| − | + | *Fourier analysis is the study of the way general functions may be represented by sums of simpler trigonometric functions. | |
| − | + | *It converts a set of numbers into another equal sized set of numbers. | |
| − | + | *It is the process of analyzing a complex wave by separating it into a plurality of component wave, each of a particular frequency, amplitude and phase displacement. | |
| − | + | *In <math>FOURIERANALYSIS(n1,n2,n3,n4,…)</math>, <math>n1,n2,n3,n4…</math>are real numbers. | |
| − | + | *But the size of the set to be a power of 2.i.e., n1,n2,n3,... the size of the numbers can be 2,4,8,16.... | |
| − | + | *So we can form the Fourier transform of a set of 64 numbers, but not a set of 50 numbers. | |
| − | + | *In the discrete Fourier Transform (DFT) decomposes the input time series into a set of cosine functions. | |
| − | + | *It is having the following properties | |
| − | + | 1.The transformed data is no longer in the time domain. | |
| − | + | 2. The transformation operates on the whole data set. It is not a point-by-point transformation. | |
| − | < | + | 3.The transformed data is complex (not real-valued). |
| − | + | *So the output of this function is Hermite symmetric, which means that the positive and negative real parts will be identical, and that the positive and negative imaginary parts will be the same, but of opposite sign. | |
| − | + | *The formula for the DFT is :<math>x_m=\frac{1}{N}\sum_{k=1}^N A_k *cos(\phi_k+k*\omega*m)</math> | |
| − | + | where <math>A_k</math> is the amplitude,<math>\phi_k</math> is the phase value in radians. | |
| − | </ | + | *<math>\omega</math> is the fundamental or principal radian frequency and <math>\omega</math>=\frac{2\pi}{T}, <math>T</math> is the number of observations in the equally-spaced input time series.<math>N</math> is the is the number of pairs. |
| − | + | *This function will give the result as error when | |
| − | < | + | 1. any one of the argument is nonnumeric. |
| − | + | 2. The number of input value is not a power of 2. | |
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 02:51, 13 February 2014
FOURIERANALYSIS(n1,n2,n3,n4,…)
- Failed to parse (syntax error): {\displaystyle n1,n2,n3,n4…} are real numbers.
Description
- This function gives the value of the discrete fourier tranform.
- Fourier analysis is the study of the way general functions may be represented by sums of simpler trigonometric functions.
- It converts a set of numbers into another equal sized set of numbers.
- It is the process of analyzing a complex wave by separating it into a plurality of component wave, each of a particular frequency, amplitude and phase displacement.
- In Failed to parse (syntax error): {\displaystyle FOURIERANALYSIS(n1,n2,n3,n4,…)} , Failed to parse (syntax error): {\displaystyle n1,n2,n3,n4…} are real numbers.
- But the size of the set to be a power of 2.i.e., n1,n2,n3,... the size of the numbers can be 2,4,8,16....
- So we can form the Fourier transform of a set of 64 numbers, but not a set of 50 numbers.
- In the discrete Fourier Transform (DFT) decomposes the input time series into a set of cosine functions.
- It is having the following properties
1.The transformed data is no longer in the time domain. 2. The transformation operates on the whole data set. It is not a point-by-point transformation. 3.The transformed data is complex (not real-valued).
- So the output of this function is Hermite symmetric, which means that the positive and negative real parts will be identical, and that the positive and negative imaginary parts will be the same, but of opposite sign.
- The formula for the DFT is :
where is the amplitude, is the phase value in radians.
- is the fundamental or principal radian frequency and =\frac{2\pi}{T}, is the number of observations in the equally-spaced input time series. is the is the number of pairs.
- This function will give the result as error when
1. any one of the argument is nonnumeric. 2. The number of input value is not a power of 2.
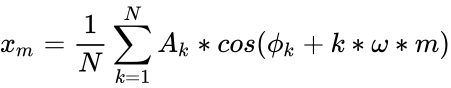
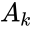 is the amplitude,
is the amplitude,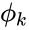 is the phase value in radians.
is the phase value in radians.
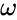 is the fundamental or principal radian frequency and
is the fundamental or principal radian frequency and 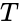 is the number of observations in the equally-spaced input time series.
is the number of observations in the equally-spaced input time series.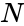 is the is the number of pairs.
is the is the number of pairs.