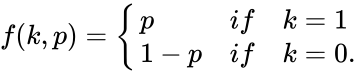Difference between revisions of "Manuals/calci/BERNOULLI"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''RANDOMNUMBERGENERATION'''(Number, RandomNumber, Distribution, NewTableFlag, ProbabilityValue) where, '''N...") |
|||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''BERNOULLIDISTRIBUTED(k,p)'''</div><br/> |
| + | *<math>k</math> represents the number of variables. | ||
| + | *<math>p</math> p is the probability value. | ||
| − | + | ==Description== | |
| + | *This function gives the value of the Bernoulli distribution. | ||
| + | *It is a discrete probability distribution. | ||
| + | *Bernoulli distribution is the theoretical distribution of the number of successes in a finite set of independent trials with a constant probability of success. | ||
| + | *The Bernoulli distribution is simply BINOM(1,P). | ||
| + | *This distribution best describes all situations where a trial is made resulting in either success or failure, such as when tossing a coin, or when modeling the success or failure. | ||
| + | *<math>BERNOULLIDISTRIBUTED(k,p)</math> ,<math>k</math> represents the number of variables. | ||
| + | *<math>p</math> is the probability value. The <math>p</math> vaule is ranges from 0 to 1. | ||
| + | *The Bernoulli distribution is defined by:<math>f(x)=p^x(1-p)^{1-x}</math>, for x=0,1, where <math>p</math> is the probability that a particular event will occur. | ||
| + | *The probability mass function is :<math>f(k,p) = \begin{cases}p &if& k=1\\ | ||
| + | 1-p &if &k=0. | ||
| + | \end{cases}</math> | ||
| + | *This function will give the result as error when | ||
| + | 1. Any one of the argument is nonnumeric. | ||
| + | 2. The value of p<0 or p>1. | ||
| − | + | ==Examples== | |
| + | #=BERNOULLIDISTRIBUTED(5,0.5)=1 1 0 0 1, 0 0 0 0 0 | ||
| + | #=BERNOULLIDISTRIBUTED(3,0.2)= 0 0 0 | ||
| − | + | ==See Also== | |
| − | + | ==References== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 22:47, 13 February 2014
BERNOULLIDISTRIBUTED(k,p)
- represents the number of variables.
- p is the probability value.
Description
- This function gives the value of the Bernoulli distribution.
- It is a discrete probability distribution.
- Bernoulli distribution is the theoretical distribution of the number of successes in a finite set of independent trials with a constant probability of success.
- The Bernoulli distribution is simply BINOM(1,P).
- This distribution best describes all situations where a trial is made resulting in either success or failure, such as when tossing a coin, or when modeling the success or failure.
- , represents the number of variables.
- is the probability value. The vaule is ranges from 0 to 1.
- The Bernoulli distribution is defined by:, for x=0,1, where is the probability that a particular event will occur.
- The probability mass function is :
- This function will give the result as error when
1. Any one of the argument is nonnumeric.
2. The value of p<0 or p>1.
Examples
- =BERNOULLIDISTRIBUTED(5,0.5)=1 1 0 0 1, 0 0 0 0 0
- =BERNOULLIDISTRIBUTED(3,0.2)= 0 0 0
 represents the number of variables.
represents the number of variables.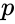 p is the probability value.
p is the probability value.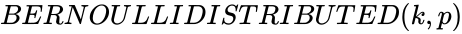 ,
,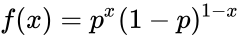 , for x=0,1, where
, for x=0,1, where