Difference between revisions of "Manuals/calci/PPMT"
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> '''PPMT'''(Rate, Period, NoPayments, PresentValue, FutureValue, Type) where, '''Rate''' - represents the inte...") |
|||
| Line 1: | Line 1: | ||
| + | <div style="font-size:30px">'''PPMT(r,pe,np,pv,fv,ty)'''</div><br/> | ||
| + | *<math>r </math> is the interest rate. | ||
| + | *<math> pe </math> is the period. | ||
| + | *<math> np </math> is the total number of payment periods. | ||
| + | *<math> pv </math> is the at present value. | ||
| + | *<math> fv </math> is the future value. | ||
| + | *<math> ty </math> is the type. | ||
| + | |||
| + | |||
| + | ==Description== | ||
| + | This function gives the payment on the principal for a given period. It is based on the period, fixed payments and a fixed interest rate. This function calculates payment for an investment or a loan with the assumption of constant payments at regular intervals and a fixed interest rate. In PPMT(r,pe,np,pv,fv,ty), r is the rate of interest for the period.Suppose we are taking a loan for 8 percent annual interest rate and paying the amount in monthly, then the r value is 8%/12. So we have to enter the r value as 8%/12 or 0.6667% or 0.006667 in to the formula as the rate.pe indicates the period and it is lying with in 1 to nper.np is the total number of payment periods in an annuity.pv is the present value-the total amount that a series of future payments is worth now.fv is the future value of an investment or loan (the value you want to achieve at the end of all periods) when we are omitting the value of fv ,then it is assumed to be 0. ty is the number 0 or 1 which is specifies the time to make a payment during the period. when we are not giving the value of ty, then it is assumed to be 0. | ||
| + | ty value Explanation | ||
| + | 0 Payments are due at the end of the period. | ||
| + | 1 Payments are due at the beginning of the period. The interest rate is divided by 12 to get a monthly rate. The number of years the money is paid out is multiplied by 12 to get the number of payments. | ||
| + | |||
| + | where where r , , , , and . | ||
| + | |||
| + | |||
| + | |||
<div id="6SpaceContent" class="zcontent" align="left"> | <div id="6SpaceContent" class="zcontent" align="left"> | ||
| Line 49: | Line 68: | ||
Lets see an example in (Column1, Row6) | Lets see an example in (Column1, Row6) | ||
| − | + | UNIQf4b9b6692e59938e-nowiki-00000004-QINU | |
PPMT returns -469.644554(the interest rate divided by 12 to get a monthly rate). | PPMT returns -469.644554(the interest rate divided by 12 to get a monthly rate). | ||
| Line 55: | Line 74: | ||
Consider another example | Consider another example | ||
| − | + | UNIQf4b9b6692e59938e-nowiki-00000005-QINU | |
It returns #ERROR(type=4). | It returns #ERROR(type=4). | ||
Revision as of 03:42, 24 February 2014
- is the interest rate.
- is the period.
- is the total number of payment periods.
- is the at present value.
- is the future value.
- is the type.
Description
This function gives the payment on the principal for a given period. It is based on the period, fixed payments and a fixed interest rate. This function calculates payment for an investment or a loan with the assumption of constant payments at regular intervals and a fixed interest rate. In PPMT(r,pe,np,pv,fv,ty), r is the rate of interest for the period.Suppose we are taking a loan for 8 percent annual interest rate and paying the amount in monthly, then the r value is 8%/12. So we have to enter the r value as 8%/12 or 0.6667% or 0.006667 in to the formula as the rate.pe indicates the period and it is lying with in 1 to nper.np is the total number of payment periods in an annuity.pv is the present value-the total amount that a series of future payments is worth now.fv is the future value of an investment or loan (the value you want to achieve at the end of all periods) when we are omitting the value of fv ,then it is assumed to be 0. ty is the number 0 or 1 which is specifies the time to make a payment during the period. when we are not giving the value of ty, then it is assumed to be 0. ty value Explanation 0 Payments are due at the end of the period. 1 Payments are due at the beginning of the period. The interest rate is divided by 12 to get a monthly rate. The number of years the money is paid out is multiplied by 12 to get the number of payments.
where where r , , , , and .
PPMT(Rate, Period, NoPayments, PresentValue, FutureValue, Type)
where,
Rate - represents the interest rate for the loan.
Period - represent the period and start from 1 to NoPayments.
NoPayments - the total number of payments period in a year.
PresentValue - represents the present value.
FutureValue - represents the future value.
If omitted cosidered as a 0.
Type - represents payments due.
Type Payment Due
0 or omitted end of the period
1 beginning of the period
It returns the paymenton the principal for agiven period for an investment based on periodic, constant interest rate and constant payments.
If Type other than 0 or 1, PPMT returns the #ERROR.
PPMT
Lets see an example in (Column1, Row6)
?UNIQf4b9b6692e59938e-nowiki-00000004-QINU?
PPMT returns -469.644554(the interest rate divided by 12 to get a monthly rate).
Consider another example
?UNIQf4b9b6692e59938e-nowiki-00000005-QINU?
It returns #ERROR(type=4).
| Column1 | Column2 | Column3 | Column4 | |
| Row1 | 20% | |||
| Row2 | 5 | |||
| Row3 | 50000 | |||
| Row4 | -469.644554 | |||
| Row5 | ||||
| Row6 |
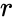 is the interest rate.
is the interest rate.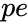 is the period.
is the period.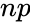 is the total number of payment periods.
is the total number of payment periods.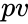 is the at present value.
is the at present value.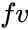 is the future value.
is the future value.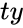 is the type.
is the type.