Difference between revisions of "Manuals/calci/LOG10"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''LOG10( | + | <div style="font-size:30px">'''LOG10(Number)'''</div><br/> |
| − | *where <math> | + | *where <math>Number</math> is the any positive real number. |
| + | |||
==Description== | ==Description== | ||
| + | |||
*This function gives the logarithm value with the base 10. | *This function gives the logarithm value with the base 10. | ||
*The logarithm of x to base b is the solution y to the equation.i.e <math>b^y=x</math>. | *The logarithm of x to base b is the solution y to the equation.i.e <math>b^y=x</math>. | ||
*For e.g The logarithm of 1000 to base 10 is 3. Because 1000 = 10*10*10 = <math>10^3</math>. | *For e.g The logarithm of 1000 to base 10 is 3. Because 1000 = 10*10*10 = <math>10^3</math>. | ||
| − | *The logarithm of base 10 is called Common Logarithm or Decimal Logarithm. | + | *The logarithm of base 10 is called Common Logarithm or Decimal Logarithm or Decadic Logarithm. |
*It is denoted by <math>\log_{10}</math> or <math>log(x)</math>. | *It is denoted by <math>\log_{10}</math> or <math>log(x)</math>. | ||
*<math>\log_{10}(x)</math> is related to the number of decimal digits of a positive integer x: the number of digits is the smallest integer strictly bigger than <math>\log_{10}(x)</math>. | *<math>\log_{10}(x)</math> is related to the number of decimal digits of a positive integer x: the number of digits is the smallest integer strictly bigger than <math>\log_{10}(x)</math>. | ||
*For e.g:log(5260)= 3.7209, that is nearly(next digit) to 4. | *For e.g:log(5260)= 3.7209, that is nearly(next digit) to 4. | ||
*That is the number of digits of 5260(4). | *That is the number of digits of 5260(4). | ||
| + | |||
| + | ==ZOS Section== | ||
| + | *The syntax is to calculate LOG10 in ZOS is <math>LOG10(Number)</math>. | ||
| + | **where <math>Number</math> is the any positive real number. | ||
| + | *For e.g.,[25..35]@LOG10. | ||
| + | *[25..50..3]@LOG10 | ||
==Examples== | ==Examples== | ||
| − | + | ||
| − | + | #=log 10(5)= 0.698970004 | |
| − | + | #=log(55)= 1.740362689 | |
| − | + | #=log(10)= 1 | |
| − | + | #=log(1)= 0 | |
| − | + | #=log(-10)= NaN | |
| + | #=log(0.25)= -0.602059991 | ||
==See Also== | ==See Also== | ||
| + | |||
*[[Manuals/calci/LN | LN ]] | *[[Manuals/calci/LN | LN ]] | ||
*[[Manuals/calci/IMLOG10 | IMLOG10 ]] | *[[Manuals/calci/IMLOG10 | IMLOG10 ]] | ||
Revision as of 04:29, 24 April 2014
LOG10(Number)
- where is the any positive real number.
Description
- This function gives the logarithm value with the base 10.
- The logarithm of x to base b is the solution y to the equation.i.e .
- For e.g The logarithm of 1000 to base 10 is 3. Because 1000 = 10*10*10 = .
- The logarithm of base 10 is called Common Logarithm or Decimal Logarithm or Decadic Logarithm.
- It is denoted by or .
- is related to the number of decimal digits of a positive integer x: the number of digits is the smallest integer strictly bigger than .
- For e.g:log(5260)= 3.7209, that is nearly(next digit) to 4.
- That is the number of digits of 5260(4).
ZOS Section
- The syntax is to calculate LOG10 in ZOS is .
- where is the any positive real number.
- For e.g.,[25..35]@LOG10.
- [25..50..3]@LOG10
Examples
- =log 10(5)= 0.698970004
- =log(55)= 1.740362689
- =log(10)= 1
- =log(1)= 0
- =log(-10)= NaN
- =log(0.25)= -0.602059991
See Also
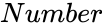 is the any positive real number.
is the any positive real number. .
.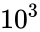 .
. or
or 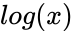 .
.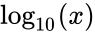 is related to the number of decimal digits of a positive integer x: the number of digits is the smallest integer strictly bigger than
is related to the number of decimal digits of a positive integer x: the number of digits is the smallest integer strictly bigger than 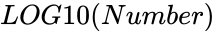 .
.