Difference between revisions of "Manuals/calci/MANNWHITNEYUTEST"
Jump to navigation
Jump to search
| Line 19: | Line 19: | ||
*Suppose the two groups of the populations have distributions with the same shape it can be viewed as a comparison of two medians.With out the assumption the Mann-Whitney test does not compare medians. | *Suppose the two groups of the populations have distributions with the same shape it can be viewed as a comparison of two medians.With out the assumption the Mann-Whitney test does not compare medians. | ||
*To find statistic value of this test the steps are required: | *To find statistic value of this test the steps are required: | ||
| − | *1.For the two observations of values, find the rank all together. | + | **1.For the two observations of values, find the rank all together. |
| − | *2.Add up all the ranks in a first observation. | + | **2.Add up all the ranks in a first observation. |
| − | *3.Add up all the ranks in a second group. | + | **3.Add up all the ranks in a second group. |
| − | *4.Select the larger rank. | + | **4.Select the larger rank. |
| − | *5.Calculate the number of participants,number of people in each group. | + | **5.Calculate the number of participants,number of people in each group. |
| − | *6.Calculate the test statistic:<math>U=\frac{n_1*n_2+nx(nx+1)}{2-Tx}</math> | + | **6.Calculate the test statistic:<math>U=\frac{n_1*n_2+nx(nx+1)}{2-Tx}</math> |
*where <math>n_1</math> and <math>n_2</math> are number of participants and number of people. | *where <math>n_1</math> and <math>n_2</math> are number of participants and number of people. | ||
*<math>Tx</math> is the larger rank total.<math>nx</math> is the similar value of <math>n1</math>. | *<math>Tx</math> is the larger rank total.<math>nx</math> is the similar value of <math>n1</math>. | ||
| − | *7.State Result: In this step we have to take a decision of null hypothesis either accept or reject depending on the z value using critical value table. | + | **7.State Result: In this step we have to take a decision of null hypothesis either accept or reject depending on the z value using critical value table. |
| − | *8.State Conclusion: To be significant, our obtained U has to be equal to or LESS than this | + | **8.State Conclusion: To be significant, our obtained U has to be equal to or LESS than this |
| − | critical value. | + | critical value. |
==Example== | ==Example== | ||
Revision as of 23:04, 15 May 2014
MANNWHITNEYUTEST(xRange,yRange,Confidencelevel,Logicalvalue)
- is the array of x values.
- is the array of y values.
- is the value between 0 and 1.
- is either TRUE or FALSE.
Description
- This function gives the test statistic value of the Mann Whitey U test.
- It is one type of Non parametric test.It is also called Mann–Whitney–Wilcoxon,Wilcoxon rank-sum test or Wilcoxon–Mann–Whitney test.
- Using this test we can analyze rank-ordered data.
- This test is alternative to the independent-sample, Student t test, and yields results identical to those obtained from the Wilcoxon Two Independent Samples Test.
- This test is used to compare differences between two independent groups when the dependent variable is either ordinal or continuous, but not normally distributed.
- Mann whitey u test is having the following properties:
- 1.Data points should be independent from each other.
- 2.Data do not have to be normal and variances do not have to be equal.
- 3.All individuals must be selected at random from the population.
- 4.All individuals must have equal chance of being selected.
- 5.Sample sizes should be as equal as possible but for some differences are allowed.
- Suppose the two groups of the populations have distributions with the same shape it can be viewed as a comparison of two medians.With out the assumption the Mann-Whitney test does not compare medians.
- To find statistic value of this test the steps are required:
- 1.For the two observations of values, find the rank all together.
- 2.Add up all the ranks in a first observation.
- 3.Add up all the ranks in a second group.
- 4.Select the larger rank.
- 5.Calculate the number of participants,number of people in each group.
- 6.Calculate the test statistic:
- where and are number of participants and number of people.
- is the larger rank total. is the similar value of .
- 7.State Result: In this step we have to take a decision of null hypothesis either accept or reject depending on the z value using critical value table.
- 8.State Conclusion: To be significant, our obtained U has to be equal to or LESS than this
critical value.
Example
| A | B | |
|---|---|---|
| 1 | 20 | 22 |
| 2 | 15 | 17 |
| 3 | 25 | 19 |
| 4 | 35 | 38 |
| 5 | 17 | 16 |
=MANNWHITNEYUTEST(A1:A5,B1:B5,0.05,TRUE)
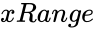 is the array of x values.
is the array of x values.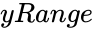 is the array of y values.
is the array of y values.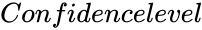 is the value between 0 and 1.
is the value between 0 and 1.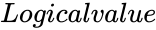 is either TRUE or FALSE.
is either TRUE or FALSE.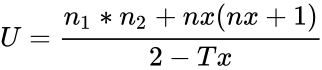
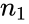 and
and 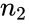 are number of participants and number of people.
are number of participants and number of people.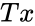 is the larger rank total.
is the larger rank total. is the similar value of
is the similar value of  .
.