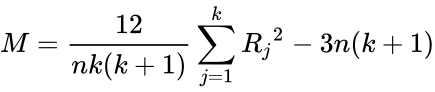Difference between revisions of "Manuals/calci/FRIEDMANTEST"
Jump to navigation
Jump to search
(Created page with "==Feature==") |
|||
| Line 1: | Line 1: | ||
| − | == | + | <div style="font-size:25px">'''FRIEDMAN(Array,SignificanceLevel,logicalValue)'''</div><br/> |
| + | *<math>Array</math> is the array of values to find the test statistic. | ||
| + | *<math>SignificanceLevel</math> is the value between 0 and 1. | ||
| + | *<math>Logicalvalue</math> is either TRUE or FALSE. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the Test statistic summary of FriedMan Test. | ||
| + | *Friedman's test is a nonparametric test that compares three or more paired groups. | ||
| + | *It is the alternative to ANOVA with repeated measures. | ||
| + | *It is used to test for differences between groups when the dependent variable being measured is ordinal. | ||
| + | *It can also be used for continuous data that has violated the assumptions necessary to run the one-way ANOVA with repeated measures. | ||
| + | *This test is simelar to the Kruskal Wallis test. | ||
| + | *The data of the Fried Man test having the following assumptions: | ||
| + | *1. One group that is measured on three or more different occasions. | ||
| + | *2.Group is a random sample from the population. | ||
| + | *3.The dependent variable should be measured at the ordinal or continuous level. | ||
| + | *4.Samples do NOT need to be normally distributed. | ||
| + | *'''Steps for Fried man Test''': | ||
| + | *1.Define Null and Alternative Hypotheses:Null Hypotheses:There is no difference between the conditions.Alternative Hypotheses:There is a difference between the conditions. | ||
| + | *2.State Alpha:Alpha=0.05. | ||
| + | *3.Calculate degrees of freedom:df = k – 1, where k = number of groups. | ||
| + | *4.State Decision Rule:From the Chi squared table calculate the critical value. | ||
| + | *Suppose the chisquared(symbol)is greater than the critical value then reject the null hypothesis | ||
| + | *5.Calculate the Test Statistic:<math>M=\frac{12}{nk(k+1)}\sum_{j=1}^k {R_j}^2-3n(k+1)</math> | ||
| + | *k = number of columns (often called “treatments”) | ||
| + | *n = number of rows (often called “blocks”) | ||
| + | *Rj = sum of the ranks in column j. | ||
| + | *If there is no significant difference between the sum of the ranks of each of the columns, then | ||
| + | M will be small, but if at least one column shows significant difference then M will be larger. | ||
| + | *6.State Results:In this step we have to take a decision of null hypothesis either accept or reject depending on the critical value table. | ||
| + | *7.State Conclusion:To be significant, our obtained U has to be equal to or LESS than this | ||
| + | critical value. | ||
| + | |||
| + | ==Example== | ||
Revision as of 22:24, 21 May 2014
FRIEDMAN(Array,SignificanceLevel,logicalValue)
- is the array of values to find the test statistic.
- is the value between 0 and 1.
- is either TRUE or FALSE.
Description
- This function gives the Test statistic summary of FriedMan Test.
- Friedman's test is a nonparametric test that compares three or more paired groups.
- It is the alternative to ANOVA with repeated measures.
- It is used to test for differences between groups when the dependent variable being measured is ordinal.
- It can also be used for continuous data that has violated the assumptions necessary to run the one-way ANOVA with repeated measures.
- This test is simelar to the Kruskal Wallis test.
- The data of the Fried Man test having the following assumptions:
- 1. One group that is measured on three or more different occasions.
- 2.Group is a random sample from the population.
- 3.The dependent variable should be measured at the ordinal or continuous level.
- 4.Samples do NOT need to be normally distributed.
- Steps for Fried man Test:
- 1.Define Null and Alternative Hypotheses:Null Hypotheses:There is no difference between the conditions.Alternative Hypotheses:There is a difference between the conditions.
- 2.State Alpha:Alpha=0.05.
- 3.Calculate degrees of freedom:df = k – 1, where k = number of groups.
- 4.State Decision Rule:From the Chi squared table calculate the critical value.
- Suppose the chisquared(symbol)is greater than the critical value then reject the null hypothesis
- 5.Calculate the Test Statistic:
- k = number of columns (often called “treatments”)
- n = number of rows (often called “blocks”)
- Rj = sum of the ranks in column j.
- If there is no significant difference between the sum of the ranks of each of the columns, then
M will be small, but if at least one column shows significant difference then M will be larger.
- 6.State Results:In this step we have to take a decision of null hypothesis either accept or reject depending on the critical value table.
- 7.State Conclusion:To be significant, our obtained U has to be equal to or LESS than this
critical value.
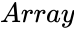 is the array of values to find the test statistic.
is the array of values to find the test statistic.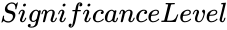 is the value between 0 and 1.
is the value between 0 and 1.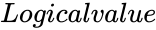 is either TRUE or FALSE.
is either TRUE or FALSE.