Difference between revisions of "Manuals/calci/LN"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''LN( | + | <div style="font-size:30px">'''LN(number)'''</div><br/> |
| − | *where <math> | + | *where <math>number</math> is the any positive real number. |
==Description== | ==Description== | ||
| Line 13: | Line 13: | ||
*The <math>ln(x)</math> is the inverse function of the exponential function <math>e^{ln(x)}=x</math> if <math>x>0</math>. | *The <math>ln(x)</math> is the inverse function of the exponential function <math>e^{ln(x)}=x</math> if <math>x>0</math>. | ||
*<math>ln(e^x)=x</math> | *<math>ln(e^x)=x</math> | ||
| + | |||
| + | ==ZOS Section== | ||
| + | *The syntax is to calculate Natural logarithm in ZOS is <math>LN(number)</math>. | ||
| + | ***where <math>number</math> is the any positive real number. | ||
| + | *For e.g.,LN(20..23) | ||
==Examples== | ==Examples== | ||
| Line 26: | Line 31: | ||
*[[Manuals/calci/LOG | LOG]] | *[[Manuals/calci/LOG | LOG]] | ||
*[[Manuals/calci/EXP | EXP]] | *[[Manuals/calci/EXP | EXP]] | ||
| − | |||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/Natural_logarithm Natural Logarithm] | [http://en.wikipedia.org/wiki/Natural_logarithm Natural Logarithm] | ||
Revision as of 23:47, 18 June 2014
LN(number)
- where is the any positive real number.
Description
- This function gives the Natural Logarithm of a number.
- is the logarithm in which the base is the irrational number (= 2.71828...).
- For example,
- It was formely also called Hyperbolic logarithm.
- And also called Napierian logarithm.
- The constant is called Euler's number.
- The Natural Logarithm is denoted by or .
- where is the Positive real number.
- The is the inverse function of the exponential function if .
ZOS Section
- The syntax is to calculate Natural logarithm in ZOS is .
- where is the any positive real number.
- For e.g.,LN(20..23)
Examples
- =LN(15) = 2.708050201
- =LN(8.3) = 2.116255515
- =LN(1) = 0
- =LN(0) = INFINITY
- =LN(-20) = NAN
- =LN(exp(5)) = 5
- =EXP(LN(7)) = 7
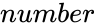 is the any positive real number.
is the any positive real number.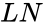 is the logarithm in which the base is the irrational number
is the logarithm in which the base is the irrational number 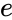 (
(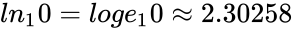
 or
or 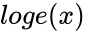 .
. is the Positive real number.
is the Positive real number.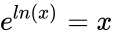 if
if 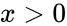 .
.
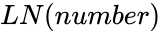 .
.