Difference between revisions of "Manuals/calci/IMLOG2"
Jump to navigation
Jump to search
| Line 27: | Line 27: | ||
==See Also== | ==See Also== | ||
*[[Manuals/calci/IMLOG10 | IMLOG10 ]] | *[[Manuals/calci/IMLOG10 | IMLOG10 ]] | ||
| − | *[[Manuals/calci/ | + | *[[Manuals/calci/LOG10 | LOG10 ]] |
*[[Manuals/calci/COMPLEX | COMPLEX ]] | *[[Manuals/calci/COMPLEX | COMPLEX ]] | ||
==References== | ==References== | ||
[http://en.wikipedia.org/wiki/Binary_logarithm Binary Logarithm] | [http://en.wikipedia.org/wiki/Binary_logarithm Binary Logarithm] | ||
Revision as of 23:20, 24 June 2014
IMLOG2(Complexnumber)
- is of the form
Description
- This function gives the binary logarithm of a complex number.
- , where Complexnumber is in the form of . i.e. & are the real numbers.
- And is the imaginary unit ..
- Binary logarithm is the inverse function of Failed to parse (syntax error): {\displaystyle n ↦ 2n} .
- Log base 2 is called Binary logarithm.
- To find the Binary logarithm of a complex number we have to calculate from the natural logarithm.
- So .
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
ZOS Section
- The syntax is to calculate Binary logarithm of a complex number is .
- is of the form .
- For e.g imlog2("2.1-3.5i")
Examples
- =IMLOG2("2+3i") = 1.85021985921295+1.41787163085485i
- =IMLOG2("5-6i") = 2.96536866900967-1.26388460522614i
- =IMLOG2("15") = 3.90689059590921
- =IMLOG2("11i") = 3.45943161890355+2.26618007108801i
- =IMLOG2("0") = NULL
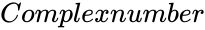 is of the form
is of the form 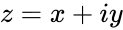
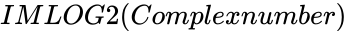 , where Complexnumber is in the form of
, where Complexnumber is in the form of  &
& 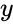 are the real numbers.
are the real numbers.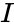 is the imaginary unit .
is the imaginary unit .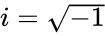 .
.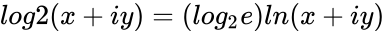 .
.