Difference between revisions of "Manuals/calci/ERFC"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''ERFC( | + | <div style="font-size:30px">'''ERFC(a,accuracy)'''</div><br/> |
| − | *<math> | + | *<math>a</math> is the lower limit. |
| + | *<math>accuracy</math> gives the accurate value of the solution. | ||
==Description== | ==Description== | ||
| Line 8: | Line 9: | ||
*ERFC is defined by: | *ERFC is defined by: | ||
<math>ERFC(x)=\frac{2}{\sqrt{\pi}}\int\limits_{x}^{\infty}e^{-t^2} dt=1-ERF(x)</math>. | <math>ERFC(x)=\frac{2}{\sqrt{\pi}}\int\limits_{x}^{\infty}e^{-t^2} dt=1-ERF(x)</math>. | ||
| − | *This function will return the result as error when | + | *This function will return the result as error when a is nonnumeric or negative. |
| + | |||
| + | ==ZOS Section== | ||
| + | *The syntax is to calculate complementary error function in ZOS is <math>ERFC(a,accuracy)</math>. | ||
| + | **<math>a</math> is the lower limit. | ||
| + | **<math>accuracy</math> gives the accurate value of the solution. | ||
| + | *For e.g.,erfc(10),erfc(10,0.01) | ||
==Examples== | ==Examples== | ||
Revision as of 02:51, 3 July 2014
ERFC(a,accuracy)
- is the lower limit.
- gives the accurate value of the solution.
Description
- This function gives the complementary ERF function.
- The complementary error function is the error function with the limit x and infinity. It is denoted by erfc(x).
- It is also called scaled complementary error function.
- ERFC is defined by:
.
- This function will return the result as error when a is nonnumeric or negative.
ZOS Section
- The syntax is to calculate complementary error function in ZOS is .
- is the lower limit.
- gives the accurate value of the solution.
- For e.g.,erfc(10),erfc(10,0.01)
Examples
- ERFC(3)=0.0000219610
- ERFC(2)=0.00467776242
- ERFC(0)=1
- ERFC(-2)=NAN
 is the lower limit.
is the lower limit.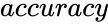 gives the accurate value of the solution.
gives the accurate value of the solution.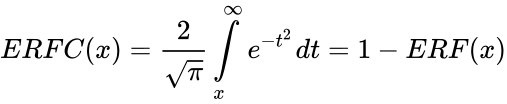 .
.
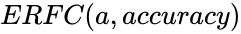 .
.