Difference between revisions of "Manuals/calci/CHOLESKY"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''CHOLESKY( | + | <div style="font-size:30px">'''CHOLESKY(arr)'''</div><br/> |
| − | *<math> | + | *<math>arr</math> is the array of numeric elements |
==Description== | ==Description== | ||
*This function gives the value of Cholesky factorization. | *This function gives the value of Cholesky factorization. | ||
| − | *It is called | + | *It is called Cholesky Decomposition or Cholesky Factorization. |
| − | *The Cholesky | + | *The Cholesky Factorization is only defined for symmetric or Hermitian positive definite matrices. |
| + | *Every positive definite matrix A can be factored as <math>A</math> = <math>LL^{T}</math> | ||
where | where | ||
<math>L</math> is lower triangular with positive diagonal elements | <math>L</math> is lower triangular with positive diagonal elements | ||
<math>L^{T}</math> is is the conjugate transpose value of <math>L</math> | <math>L^{T}</math> is is the conjugate transpose value of <math>L</math> | ||
*Every Hermitian positive-definite matrix (and thus also every real-valued symmetric positive-definite matrix) has a unique Cholesky decomposition. | *Every Hermitian positive-definite matrix (and thus also every real-valued symmetric positive-definite matrix) has a unique Cholesky decomposition. | ||
| − | *Here <math>CHOLESKY( | + | *Here <math>CHOLESKY(arr)</math>, <math>arr</math> is set of values to find the factorization value. |
Partition matrices in as | Partition matrices in as | ||
A= LL^T (Please take the description from http://www.seas.ucla.edu/~vandenbe/103/lectures/chol.pdf ) | A= LL^T (Please take the description from http://www.seas.ucla.edu/~vandenbe/103/lectures/chol.pdf ) | ||
Revision as of 05:39, 8 April 2015
CHOLESKY(arr)
- is the array of numeric elements
Description
- This function gives the value of Cholesky factorization.
- It is called Cholesky Decomposition or Cholesky Factorization.
- The Cholesky Factorization is only defined for symmetric or Hermitian positive definite matrices.
- Every positive definite matrix A can be factored as =
where
is lower triangular with positive diagonal elements is is the conjugate transpose value of
- Every Hermitian positive-definite matrix (and thus also every real-valued symmetric positive-definite matrix) has a unique Cholesky decomposition.
- Here , is set of values to find the factorization value.
Partition matrices in as A= LL^T (Please take the description from http://www.seas.ucla.edu/~vandenbe/103/lectures/chol.pdf )
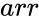 is the array of numeric elements
is the array of numeric elements =
= 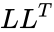
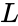 is lower triangular with positive diagonal elements
is lower triangular with positive diagonal elements
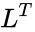 is is the conjugate transpose value of
is is the conjugate transpose value of 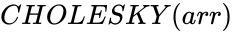 ,
,