Difference between revisions of "Manuals/calci/CHOLESKY"
Jump to navigation
Jump to search
| Line 17: | Line 17: | ||
==Examples== | ==Examples== | ||
| − | CHOLESKY([[16,32,12],[12, 18, 0],[ -5, 0, 11]]) | + | 1. =CHOLESKY([[16,32,12],[12, 18, 0],[ -5, 0, 11]]) |
{| class="wikitable" | {| class="wikitable" | ||
| Line 30: | Line 30: | ||
|} | |} | ||
| − | CHOLESKY([[25, 15, -5],[15, 18, 0],[ -5, 0, 11]]) | + | 2. =CHOLESKY([[25, 15, -5],[15, 18, 0],[ -5, 0, 11]]) |
{| class="wikitable" | {| class="wikitable" | ||
Revision as of 22:58, 8 April 2015
CHOLESKY(arr)
- is the array of numeric elements
Description
- This function gives the value of Cholesky factorization.
- It is called Cholesky Decomposition or Cholesky Factorization.
- The Cholesky Factorization is only defined for symmetric or Hermitian positive definite matrices.
- Every positive definite matrix A can be factored as =
where
is lower triangular with positive diagonal elements is is the conjugate transpose value of
- Every Hermitian positive-definite matrix has a unique Cholesky decomposition.
- Here , is set of values to find the factorization value.
- Partition matrices in as =
ZOS Section
Examples
1. =CHOLESKY([[16,32,12],[12, 18, 0],[ -5, 0, 11]])
| 4 | 0 | 0 |
| 3 | 3 | 0 |
| -1.25 | 1.25 | 2.80624 |
2. =CHOLESKY([[25, 15, -5],[15, 18, 0],[ -5, 0, 11]])
| 5 | 0 | 0 |
| 3 | 3 | 0 |
| -1 | 1 | 3 |
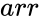 is the array of numeric elements
is the array of numeric elements =
= 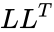
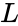 is lower triangular with positive diagonal elements
is lower triangular with positive diagonal elements
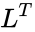 is is the conjugate transpose value of
is is the conjugate transpose value of 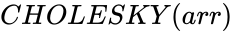 ,
,