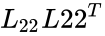Difference between revisions of "Manuals/calci/CHOLESKY"
Jump to navigation
Jump to search
| Line 34: | Line 34: | ||
</math> | </math> | ||
| − | :< | + | :<h2>Algorithm</h2> |
# Determine <math>l_{11}</math> and <math>L_{21}</math> | # Determine <math>l_{11}</math> and <math>L_{21}</math> | ||
<math>l_{11}</math> = <math>\sqrt{a_{11}}</math> | <math>l_{11}</math> = <math>\sqrt{a_{11}}</math> | ||
<math>L_{21}</math> = <math>\frac{1}{l_{11}}A_{21}</math> | <math>L_{21}</math> = <math>\frac{1}{l_{11}}A_{21}</math> | ||
| + | # Compute <math>L_{22}</math> from | ||
| + | <math>A_{22}-L{21}L{21}^{T}</math> = <math>L_{22}L{22}^{T}</math> | ||
| + | this is a Cholesky Factorization of order <math>n-1</math> | ||
==ZOS Section== | ==ZOS Section== | ||
Revision as of 05:57, 10 April 2015
CHOLESKY(arr)
- is the array of numeric elements
Description
- This function gives the value of Cholesky factorization.
- It is called Cholesky Decomposition or Cholesky Factorization.
- The Cholesky Factorization is only defined for symmetric or Hermitian positive definite matrices.
- Every positive definite matrix A can be factored as =
is lower triangular with positive diagonal elements is is the conjugate transpose value of
- Every Hermitian positive-definite matrix has a unique Cholesky decomposition.
- Here , is set of values to find the factorization value.
- Partition matrices in = is
Algorithm
- Determine and
= =
- Compute from
=
this is a Cholesky Factorization of order
ZOS Section
Examples
1. =CHOLESKY([[16,32,12],[12, 18, 0],[ -5, 0, 11]])
| 4 | 0 | 0 |
| 3 | 3 | 0 |
| -1.25 | 1.25 | 2.80624 |
2. =CHOLESKY([[25, 15, -5],[15, 18, 0],[ -5, 0, 11]])
| 5 | 0 | 0 |
| 3 | 3 | 0 |
| -1 | 1 | 3 |
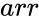 is the array of numeric elements
is the array of numeric elements =
= 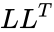
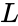 is lower triangular with positive diagonal elements
is lower triangular with positive diagonal elements
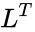 is is the conjugate transpose value of
is is the conjugate transpose value of 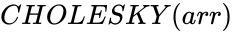 ,
, 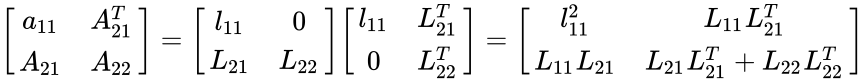
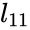 and
and 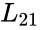

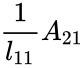
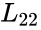 from
from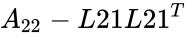 =
=