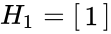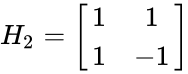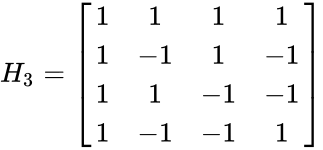Difference between revisions of "Manuals/calci/HADAMARD"
Jump to navigation
Jump to search
| Line 16: | Line 16: | ||
1 \\ | 1 \\ | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
| − | <math>H_2 = \begin{bmatrix} | + | *<math>H_2 = \begin{bmatrix} |
1 & 1 \\ | 1 & 1 \\ | ||
1 & -1 \\ | 1 & -1 \\ | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
| − | <math>H_3 =\begin{bmatrix} | + | *<math>H_3 =\begin{bmatrix} |
1 & 1 & 1 & 1 \\ | 1 & 1 & 1 & 1 \\ | ||
1 & -1 & 1 & -1\\ | 1 & -1 & 1 & -1\\ | ||
Revision as of 09:26, 24 April 2015
MATRIX("HADAMARD",order)
- is the order of the hadamard matrix.
Description
- This function gives the matrix satisfying the property of Hadamard.
- A Hadamard matrix is the square matrix with the entries of 1 and -1.
- Also the rows of that matrix are orthogonal.
- So H be a Hadamard matrix of order 2n.
- The transpose of H is closely related to its inverse.
- The equivalent definition for hadamard matrix is:
where is the n × n identity matrix and is the transpose of H.
- So the possible order of the matrix is 1,2 or positive multiple of 4.
- The few examples of hadamard matrices are:
 is the order of the hadamard matrix.
is the order of the hadamard matrix.
 is the n × n identity matrix and
is the n × n identity matrix and 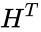 is the transpose of H.
is the transpose of H.