Difference between revisions of "Manuals/calci/HERMITIAN"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''HERMITIAN'''</div><br/>") |
|||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''HERMITIAN'''</div><br/> | + | <div style="font-size:30px">'''MATRIX("HERMITIAN",order)'''</div><br/> |
| + | *<math>order</math> is the order of the Hermitian matrix. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the Hermitian matrix of order 3. | ||
| + | *A Hermitian matrix is defined as the square matrix with complex entries which is equal to its own conjugate transpose. | ||
| + | *i.e., the matrix A is Hermitian if and only if A=A^T, where A^T denotes the conjugate transpose, which is equivalent to the condition a_(ij)=a^__(ji). | ||
| + | *A hermetian matrix is also called as self-adjoint matrix. | ||
| + | *The following matrix is the example of 3x3 Hermitian matrix: | ||
| + | <math>\begin{bmatrix} | ||
| + | 2 & 2+i & 4 \\ | ||
| + | 2-i & 3 & i \\ | ||
| + | 4 & -i & 1 \\ | ||
| + | \end{bmatrix}</math>. | ||
| + | *The diagonal elements must be real, as they must be their own complex conjugate. | ||
| + | *An integer or real matrix is Hermitian iff it is symmetric. | ||
| + | *In calci, users can change the order and number of the Hermitian matrices. | ||
| + | |||
| + | ==Examples== | ||
| + | *1.MATRIX("hermitian") | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | -62 || -48 + 4i || 49 + -40i | ||
| + | |- | ||
| + | | -48 + -4i|| -54 || 0 + 34i | ||
| + | |- | ||
| + | | 49 + 40i || 0 + -34i || -33 | ||
| + | |} | ||
| + | *2.MATRIX("hermitian",5) | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | -90 || -75 + 79i|| 56 + -17i || 92 + -51i || -13 + -21i | ||
| + | |- | ||
| + | | -75 + -79i|| -19 || -77 + -19i || 42 + 47i || 83 + -95i | ||
| + | |- | ||
| + | | 56 + 17i|| -77 + 19i || -60 || -25 + -26i || 88 + -81i | ||
| + | |- | ||
| + | | 92 + 51i || 42 + -47i || -25 + 26i || -89 || -70 + -92i | ||
| + | |- | ||
| + | | -13 + 21i || 83 + 95i || 88 + 81i || -70 + 92i || -7 | ||
| + | |} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/ANTIDIAGONAL| ANTIDIAGONAL]] | ||
| + | *[[Manuals/calci/CONFERENCE| CONFERENCE]] | ||
| + | *[[Manuals/calci/CIRCULANT| CIRCULANT]] | ||
| + | *[[Manuals/calci/HANKEL| HANKEL]] | ||
| + | |||
| + | ==References== | ||
Revision as of 11:15, 24 April 2015
MATRIX("HERMITIAN",order)
- is the order of the Hermitian matrix.
Description
- This function gives the Hermitian matrix of order 3.
- A Hermitian matrix is defined as the square matrix with complex entries which is equal to its own conjugate transpose.
- i.e., the matrix A is Hermitian if and only if A=A^T, where A^T denotes the conjugate transpose, which is equivalent to the condition a_(ij)=a^__(ji).
- A hermetian matrix is also called as self-adjoint matrix.
- The following matrix is the example of 3x3 Hermitian matrix:
.
- The diagonal elements must be real, as they must be their own complex conjugate.
- An integer or real matrix is Hermitian iff it is symmetric.
- In calci, users can change the order and number of the Hermitian matrices.
Examples
- 1.MATRIX("hermitian")
| -62 | -48 + 4i | 49 + -40i |
| -48 + -4i | -54 | 0 + 34i |
| 49 + 40i | 0 + -34i | -33 |
- 2.MATRIX("hermitian",5)
| -90 | -75 + 79i | 56 + -17i | 92 + -51i | -13 + -21i |
| -75 + -79i | -19 | -77 + -19i | 42 + 47i | 83 + -95i |
| 56 + 17i | -77 + 19i | -60 | -25 + -26i | 88 + -81i |
| 92 + 51i | 42 + -47i | -25 + 26i | -89 | -70 + -92i |
| -13 + 21i | 83 + 95i | 88 + 81i | -70 + 92i | -7 |
 is the order of the Hermitian matrix.
is the order of the Hermitian matrix.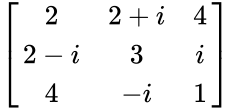 .
.