Difference between revisions of "Manuals/calci/HILBERT"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''HILBERT'''</div><br/>") |
|||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''HILBERT'''</div><br/> | + | <div style="font-size:30px">'''MATRIX("HILBERT",order)'''</div><br/> |
| + | *<math>order</math> is the order of the Hilbert matrix. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives matrix of order 3x3 with the property of Hilbert. | ||
| + | *A Hilbert matrix, is a square matrix with entries being the unit fractions. i.e.,<math>H_{ij}=\frac{1}{i+j-1}. | ||
| + | *Example for 5x5 Hilbert matrix is: <math><math>\begin{bmatrix} | ||
| + | 1 & \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} \\ | ||
| + | \frac{1}{2} & \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6} \\ | ||
| + | \frac{1}{3} & \frac{1}{4} & \frac{1}{5} & \frac{1}{6} & \frac{1}{7} \\ | ||
| + | \frac{1}{4} & \frac{1}{5} & \frac{1}{6} & \frac{1}{7} & \frac{1}{8} \\ | ||
| + | \frac{1}{5} & \frac{1}{6} & \frac{1}{7} & \frac{1}{8} & \frac{1}{9} \\ | ||
| + | \end{bmatrix}</math>. | ||
| + | *The Hilbert matrix is an example of a Hankel matrix. | ||
| + | *The Hilbert matrix is symmetric and positive definite. | ||
| + | *Also Hilbert matrices are canonical examples of ill-conditioned matrices, making them notoriously difficult to use in numerical computation. | ||
| + | *Here MATRIX("hilbert") gives the hilbert matrices with a decimal places . | ||
| + | *i.e., For 1/2 it will show 0.5, 1/3 will show 0.333 and so on. | ||
Revision as of 12:41, 24 April 2015
MATRIX("HILBERT",order)
- is the order of the Hilbert matrix.
Description
- This function gives matrix of order 3x3 with the property of Hilbert.
- A Hilbert matrix, is a square matrix with entries being the unit fractions. i.e.,.
- The Hilbert matrix is an example of a Hankel matrix.
- The Hilbert matrix is symmetric and positive definite.
- Also Hilbert matrices are canonical examples of ill-conditioned matrices, making them notoriously difficult to use in numerical computation.
- Here MATRIX("hilbert") gives the hilbert matrices with a decimal places .
- i.e., For 1/2 it will show 0.5, 1/3 will show 0.333 and so on.
 is the order of the Hilbert matrix.
is the order of the Hilbert matrix.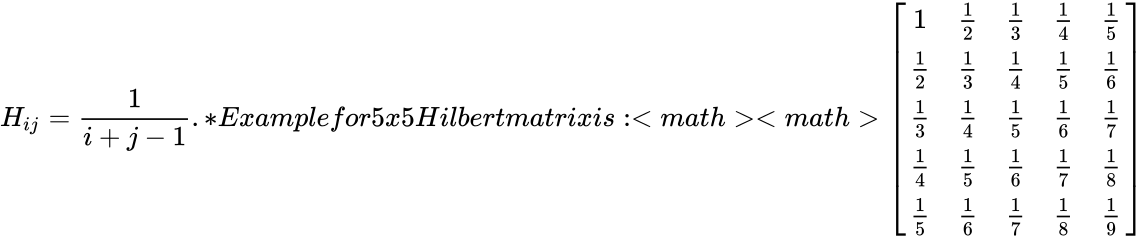 .
.